题目内容
如图，在?ABCD的面积是12，点E，F在AC上，且AE=EF=FC，则△BEF的面积为
- A.2
- B.3
- C.4
- D.6
A
分析：根据平行四边形的性质可知△ABC的面积是平行四边形面积的一半，再进一步确定△BER和△ABC的面积关系即可．
解答：∵S?ABCD=12
∴S△ABC=
S?ABCD=6，
∴S△ABC=×AC×高=×3EF×高=6，得到：×EF×高=2，
∵△BEF的面积=×EF×高=2．
∴△BEF的面积为2．
故选A．
点评：平行四边形的对角线将平行四边形分成面积相等的两个三角形，本题解题关键是利用三角形的面积计算公式找出所求三角形与已知三角形的面积关系．
分析：根据平行四边形的性质可知△ABC的面积是平行四边形面积的一半，再进一步确定△BER和△ABC的面积关系即可．
解答：∵S?ABCD=12
∴S△ABC=
S?ABCD=6，∴S△ABC=
×AC×高=×3EF×高=6，得到：×EF×高=2，∵△BEF的面积=
×EF×高=2．∴△BEF的面积为2．
故选A．
点评：平行四边形的对角线将平行四边形分成面积相等的两个三角形，本题解题关键是利用三角形的面积计算公式找出所求三角形与已知三角形的面积关系．
练习册系列答案
名校课堂系列答案
相关题目
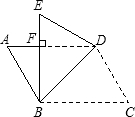如图，在?ABCD的纸片中，∠A=60°，AB=2cm，若将纸片沿BD折叠，点C落在点E的位置，AD与BE交于点F，且BE⊥AD．则BD的长为
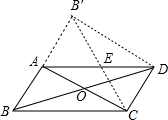到△AB′C．
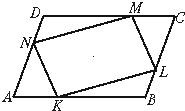7、如图，在□ABCD的各边AB、BC、CD、DA上，分别取点K、L、M、N，使AK=CM、BL=DN，则四边形KLMN为平行四边形吗？说明理由．