题目内容
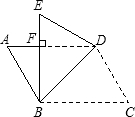如图，在?ABCD的纸片中，∠A=60°，AB=2cm，若将纸片沿BD折叠，点C落在点E的位置，AD与BE交于点F，且BE⊥AD．则BD的长为分析：由四边形ABCD是平行四边形与BE⊥AD，可证得△BFD是等腰直角三角形，由AB=2cm，∠A=60°，在Rt△ABF中，利用勾股定理即可求得BF的长，继而求得BD的长．
解答：解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∵BE⊥AD，
∴∠AFB=∠DFB=∠FBC=90°，
∵∠A=60°，∠FBD=∠CBD，
∴∠ABF=30°，∠FBD=∠DBC=45°，
∴∠FBD=∠FDB=45°，
∴FB=FD，
∵AB=2cm，
∴AF=1cm，BF=
cm，
∴DF=
cm，
∴BD=
=
cm．
故答案为：
．
∴AD∥BC，
∵BE⊥AD，
∴∠AFB=∠DFB=∠FBC=90°，
∵∠A=60°，∠FBD=∠CBD，
∴∠ABF=30°，∠FBD=∠DBC=45°，
∴∠FBD=∠FDB=45°，
∴FB=FD，
∵AB=2cm，
∴AF=1cm，BF=
| 3 |
∴DF=
| 3 |
∴BD=
| BF2+FD2 |
| 6 |
故答案为：
| 6 |
点评：此题考查了折叠的性质，矩形的性质，直角三角形的性质等知识．此题难度适中，解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
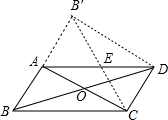到△AB′C．
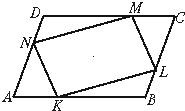7、如图，在□ABCD的各边AB、BC、CD、DA上，分别取点K、L、M、N，使AK=CM、BL=DN，则四边形KLMN为平行四边形吗？说明理由．