题目内容
【题目】如图，等边△A1C1C2的周长为1，作C1D1⊥A1C2于D1 ， 在C1C2的延长线上取点C3 ， 使D1C3=D1C1 ， 连接D1C3 ， 以C2C3为边作等边△A2C2C3；作C2D2⊥A2C3于D2 ， 在C2C3的延长线上取点C4 ， 使D2C4=D2C2 ， 连接D2C4 ， 以C3C4为边作等边△A3C3C4；…且点A1 ， A2 ， A3 ， …都在直线C1C2同侧，如此下去，则△A1C1C2 ， △A2C2C3 ， △A3C3C4 ， …，△AnCnCn+1的周长和为 ． （n≥2，且n为整数）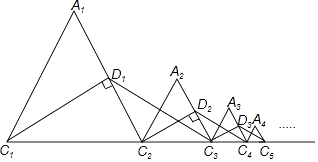
【答案】
【解析】∵等边△A1C1C2的周长为1，作C1D1⊥A1C2于D1，
∴A1D1=D1C2，
∴△A2C2C3的周长= 
△A1C1C2的周长= ，
∴△A1C1C2，△A2C2C3，△A3C3C4，…，△AnCnCn+1的周长分别为1， ， 
，…， 
，
∴△A1C1C2，△A2C2C3，△A3C3C4，…，△AnCnCn+1的周长和为1+ + +…+ = 
．
所以答案是 ．
【考点精析】关于本题考查的等边三角形的性质，需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案．
练习册系列答案
相关题目
