题目内容
△ABC中，∠C=90°，AC=
，∠A的角平分线交BC于D，且AD=
，则tanA的值为
- A.
- B.
- C.
- D.
B
分析：首先由已知，根据勾股定理求出CD，然后求出tan∠CAD=，得∠CAD=30°，又由已知AD平分∠BAC，得∠BAC=60°，从求出tanA的值．
解答：
解：在直角三角形ACD中，
由勾股定理得：
CD2=AD2-AC2=
-
=
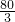-20=
，
∴CD=
，
∴
=
=，
即tan∠CAD=，
∴∠CAD=30°，
又，∠A的角平分线交BC于D，
∴∠BAD=∠CAD=30°，
∴∠BAC=∠BAD+∠CAD=60°，
∴tanA=tan60°=，
故选：B．
点评：此题考查的知识点是解直角三角形，由已知先求出CD，再求出tan∠CAD=，得出∠CAD=30°是关键．
分析：首先由已知，根据勾股定理求出CD，然后求出tan∠CAD=
，得∠CAD=30°，又由已知AD平分∠BAC，得∠BAC=60°，从求出tanA的值．解答：
解：在直角三角形ACD中，由勾股定理得：
CD2=AD2-AC2=
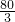-=-20=，∴CD=
，∴
==，即tan∠CAD=
，∴∠CAD=30°，
又，∠A的角平分线交BC于D，
∴∠BAD=∠CAD=30°，
∴∠BAC=∠BAD+∠CAD=60°，
∴tanA=tan60°=
，故选：B．
点评：此题考查的知识点是解直角三角形，由已知先求出CD，再求出tan∠CAD=
，得出∠CAD=30°是关键． 
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，AC=2，AB=3，D是AC上一点，E是AB上一点，且∠ADE=∠B，设AD=x，AE=y，则y与x之间的函数关系式是（ ）A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
如图，在△ABC中，AB=8，AC=6，BC=7，点D在AC上，AD=2，