Question

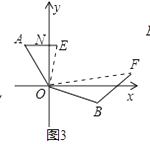
【题目】如图，在平面直角坐标系中，点A(a，0)，B(b，0)，且+| b-6|=0.

（1）求A，B的坐标；

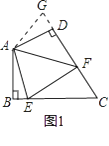
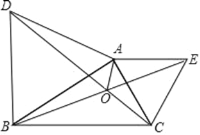
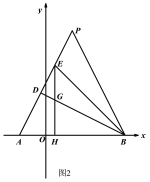
（2）如图2，点P为AB的垂直平分线上一点，BD⊥AP于点D，BE是△PBD的角平分线，EH⊥AB于点H，交BD于点G，若AD=m，DE=n，求△BEG的面积（用含m，n的式子表示）；

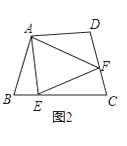
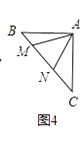
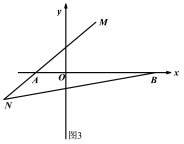
（3）如图3，点M在AB的垂直平分线上，且∠MAB=40°，点N在MA的延长线上，且MN=8，求∠ABN的度数.

Answer 1

【答案】（1）A（-2，0）B（6，0）；（2）；（3）∠ABN=10°.

【解析】

（1）由平方和绝对值的非负性即可求解a和b的值；

（2）∠EBH=∠EBG+∠GBH=∠PBD+90°-∠PAB=(90°-∠P)+ 90°-(180°-∠P)=45°，则EH=BH，可证明△EAH≌△BGH，则AE=GB，再利用三角形面积公式即可求解；

（3）连接MB，作∠BMN内部作∠BMK=40°，并取MK=8，连接KB，KN，易证△NMK为等边三角形，然后证△AMB≌△MBK，得BK=BM，由△BMN≌△BKN得∠BNM=30°，∠ABN=∠MAB-∠MNB=10°.

解：（1）由题干得，3a+b=0，b-6=0，解得，a=-2，b=6，则A（-2，0）B（6，0）；

（2）由图可知∠EBH=∠EBG+∠GBH=∠PBD+90°-∠PAB=(90°-∠P)+ 90°-(180°-∠P)=45°，由于RT△EHB，故△EHB是直角等腰三角形，则EH=BH，

∵∠AEH+∠EAH=∠GBH+∠EAH=90°，

∴∠AEH=∠GBH，

又∵∠EHA=∠BHG=90°，EH=BH，

∴△EAH≌△BGH，

∴AE=GB=m+n，

∴△BEG的面积=BG×DE=.

（3）连接MB，作∠BMN内部作∠BMK=40°，并取MK=8，连接KB，KN，

∵MA=MB，

∴∠MAB=∠MBA=40°，

∴∠ABM=180°-2×40°=100°，

∴∠NMK=∠AMB-∠BMK=100°-40°=60°，

∵MN=MK，

∴△MNK是等边三角形，

∴MN=KN，∠MNK=60°，

∵MB=MA，MK=MN=AB=8，∠BMK=∠MAB=40°

∴△AMB≌△MBK，

∴BK=BM，

∵MN=KN，BK=BM，NB=NB，

∴△BMN≌△BKN，

∴∠BNM=30°，

∴∠ABN=∠MAB-∠MNB=10°.