题目内容
17.如果3+$\sqrt{5}$的小数部分是a,5-$\sqrt{7}$的整数部分是b,那么a+b的平方应该等于5.分析 先对$\sqrt{5}$估算出大小,求出3+$\sqrt{5}$的整数部分,从而得出3+$\sqrt{5}$的小数部分a,再估算出-$\sqrt{7}$的取值范围,得出5-$\sqrt{7}$的整数部分b,然后代值计算再平方即可得出答案.
解答 解:∵2<$\sqrt{5}$<3,
∴5<3+$\sqrt{3}$<6,
∴3+$\sqrt{5}$的整数部分5,
∴3+$\sqrt{5}$的小数部分a=3+$\sqrt{5}$-5=$\sqrt{5}$-2,
∵2<$\sqrt{7}$<3,
∴-3<-$\sqrt{7}$<-2,
∴2<5-$\sqrt{7}$<3,
∴5-$\sqrt{7}$的整数部分是b=2,
∴a+b=$\sqrt{5}$-2+2=$\sqrt{5}$,
∴a+b的平方应该等于5.
故答案为:5.
点评 本题主要考查了无理数大小的估算,能够正确估算出3+$\sqrt{5}$和5-$\sqrt{7}$的大小是解决此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.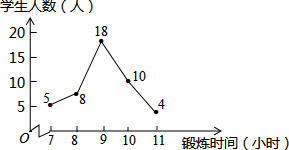 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )| A. | 18,18 | B. | 9,9 | C. | 9,10 | D. | 18,9 |
12.使式子$\sqrt{1-a}$有意义的a的范围是( )
| A. | a≥0 | B. | a≤0 | C. | a≥1 | D. | a≤1 |
2.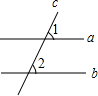 如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
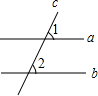 如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
9.已知一个正n边形的一个内角是它外角的5倍,则n等于( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
2.国际象棋决赛在甲乙两名选手之间进行,比赛规则是:共下10局棋,每局胜方得1分,负方得0分,平局则各得0.5分,谁的积分先达到5.5分便夺冠,不继续比赛;若10局棋下完双方积分相同,则继续下,直到分出胜负为止.下完8局时,甲4胜1平.若以前8局棋取胜的频率为各自取胜的概率,那么在后面的两局棋中,甲夺冠的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{8}$ | C. | $\frac{45}{64}$ | D. | $\frac{49}{64}$ |
 解不等式组$\left\{\begin{array}{l}{2(x-2)≤3(x-1)}\\{\frac{x}{3}<\frac{x+1}{4}}\end{array}\right.$,并把它的解集表示在数轴上.
解不等式组$\left\{\begin{array}{l}{2(x-2)≤3(x-1)}\\{\frac{x}{3}<\frac{x+1}{4}}\end{array}\right.$,并把它的解集表示在数轴上.