题目内容
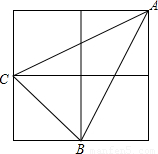
如图小正方形的边长为1，连接小正方形的三个顶点得到&△ABC，求下列问题：（1）△ABC的周长是多少？
（2）AC边上高是多少？（结果用最简二次根式表示）
【答案】分析：（1）先根据网格图，结合勾股定理可求AB、AC，以及BC的长，进而可求△ABC的周长；
（2）先根据图形面积之间的关系，可求S△ABC，再结合三角形的面积公式，易求高．
解答：解：（1）由勾股定理得AC=AB=
，BC=
，
∴△ABC的周长=AB+AC+BC=2
+
；
（2）∵S△ABC=4-
×1×2-
×1×2-
×1×1=
，
AC=
，
∴AC边上高=
×2÷
=
．
点评：本题考查了二次根式的应用、勾股定理，解题的关键是先根据勾股定理求出AC、AB、BC的长．
（2）先根据图形面积之间的关系，可求S△ABC，再结合三角形的面积公式，易求高．
解答：解：（1）由勾股定理得AC=AB=
，BC=，∴△ABC的周长=AB+AC+BC=2
+；（2）∵S△ABC=4-
×1×2-×1×2-×1×1=，AC=
，∴AC边上高=
×2÷=．点评：本题考查了二次根式的应用、勾股定理，解题的关键是先根据勾股定理求出AC、AB、BC的长．
练习册系列答案
名校课堂系列答案
相关题目
如图，正方形的边长为a，小圆的直径是b，S表示正方形面积与大圆面积的差，A是小圆面积，设圆周率为π，则
如图小正方形的边长为1，连接小正方形的三个顶点得到&△ABC，求下列问题：
+b+c的正方形来研究．
如图小正方形的边长为1，连接小正方形的三个顶点得到&△ABC，求下列问题：