题目内容
若三角形的三边满足a：b：c=5：12：13，则这个三角形中最大的角为________度．
90
分析：一个三角形的三边符合a2+b2=c2，根据勾股定理的逆定理，这个三角形是直角三角形，依此可得这个三角形中最大的角的度数．
解答：设三角形的三边分别为5x，12x，13x，则
（5x）2+（12x）2=（13x）2，
根据勾股定理的逆定理，这个三角形是直角三角形．
则这个三角形中最大的角为90度．
故答案为：90．
点评：考查了勾股定理的逆定理，解答此题要用到勾股定理的逆定理：已知三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．
分析：一个三角形的三边符合a2+b2=c2，根据勾股定理的逆定理，这个三角形是直角三角形，依此可得这个三角形中最大的角的度数．
解答：设三角形的三边分别为5x，12x，13x，则
（5x）2+（12x）2=（13x）2，
根据勾股定理的逆定理，这个三角形是直角三角形．
则这个三角形中最大的角为90度．
故答案为：90．
点评：考查了勾股定理的逆定理，解答此题要用到勾股定理的逆定理：已知三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．
练习册系列答案
相关题目
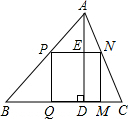其余两个顶点分别在AB，AC上．问加工成的正方形零件的边长为多少mm？”