题目内容
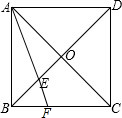 如图,正方形ABCD的对角线交于点O.AE平分∠BAC交AB于点E,交BC于点F,求证:CF=2OE.
如图,正方形ABCD的对角线交于点O.AE平分∠BAC交AB于点E,交BC于点F,求证:CF=2OE.考点:三角形中位线定理,等腰三角形的判定与性质,正方形的性质
专题:证明题
分析:作OH∥BC,交AF于点H,根据三角形中位线定理证明OH=
CF,然后根据三角形的外角的性质证明∠OHE=∠AEO,则OE=OH,据此即可证得.
| 1 |
| 2 |
解答: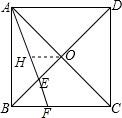 证明:作OH∥BC,交AF于点H.
证明:作OH∥BC,交AF于点H.
∵OH∥BC,且正方形ABCD中,AO=OC,
∴AH=HF,即OH是△ACF的中位线.
∴OH=
CF.
∵HO∥BC,
∴∠AOH=∠ACB=45°,
∴∠OHE=∠AOH+∠FAC=45°+∠FAC,
又∵∠AEO=∠ABD+∠BAE=45°+∠BAE,
∠FAC=∠BAE,
∴∠OHE=∠AEO,
∴OE=OH,
∴CF=2OE.
 证明:作OH∥BC,交AF于点H.
证明:作OH∥BC,交AF于点H.∵OH∥BC,且正方形ABCD中,AO=OC,
∴AH=HF,即OH是△ACF的中位线.
∴OH=
| 1 |
| 2 |
∵HO∥BC,
∴∠AOH=∠ACB=45°,
∴∠OHE=∠AOH+∠FAC=45°+∠FAC,
又∵∠AEO=∠ABD+∠BAE=45°+∠BAE,
∠FAC=∠BAE,
∴∠OHE=∠AEO,
∴OE=OH,
∴CF=2OE.
点评:本题考查了三角形的外角的性质以及三角形的中位线定理,正确通过三角形的中位线定理把题目转化为证明线段相等的问题是关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
绵阳科技城是四川省第二大城市,2012年国民生产总值约为14000000万元,用科学记数法表示应为( )万元.
| A、14×107 |
| B、1.4×107 |
| C、1.4×106 |
| D、0.14×107 |
数据160000000用科学记数法表示为( )
| A、16×107 |
| B、1.6×107 |
| C、1.6×108 |
| D、1.6×109 |
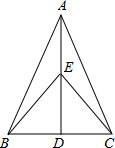 如图,在ABC中,AB=AC,点D是BC的中点,点E在AD上,求证:BE=CE.
如图,在ABC中,AB=AC,点D是BC的中点,点E在AD上,求证:BE=CE. ?
?
 如图,菱形ABCD的边长为5,对角线AC=6.则菱形ABCD的面积为
如图,菱形ABCD的边长为5,对角线AC=6.则菱形ABCD的面积为 如图是抛物线拱桥,已知水位在AB位置时,水面宽4
如图是抛物线拱桥,已知水位在AB位置时,水面宽4