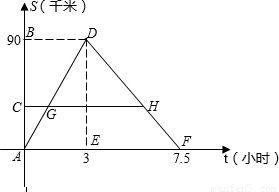
题目内容
 某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:
某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:(1)船只从码头A→B航行的速度为
30
30
千米/时;船只从码头B→A,航行的速度为20
20
千米/时;(2)过点C作CH∥t轴,分别交AD、DF于点G、H,设AC=x,GH=y,求出y与x之间的函数关系式.
分析:(1)根据图象,得到两地之间的距离和时间,根据公式即可求出船航行的速度;
(2)先判断出△DGH∽△DAF,从而得到
=
,即
=
,整理后即可得y=7.5-
x.
(2)先判断出△DGH∽△DAF,从而得到
| GH |
| AF |
| DM |
| DE |
| y |
| 7.5 |
| 90-x |
| 90 |
| 7.5 |
| 90 |
解答:解:(1)船只从码头A→B,航行速度为:90÷3=30千米/时;
船只从码头B→A,航行速度为:90÷(7.5-3)=20千米/时;
(2)设CH交DE于M,ME=AC=x,DM=90-x,
∵GH∥AF,
∴△DGH∽△DAF,
∴
=
,
即
=
,
∴y=7.5-
x,
∴y=
-
x,
∴y与x之间的函数关系式y=-
x+
.

故答案为:30、20.
船只从码头B→A,航行速度为:90÷(7.5-3)=20千米/时;
(2)设CH交DE于M,ME=AC=x,DM=90-x,
∵GH∥AF,
∴△DGH∽△DAF,
∴
| GH |
| AF |
| DM |
| DE |
即
| y |
| 7.5 |
| 90-x |
| 90 |
∴y=7.5-
| 7.5 |
| 90 |
∴y=
| 15 |
| 2 |
| 1 |
| 12 |
∴y与x之间的函数关系式y=-
| 1 |
| 12 |
| 15 |
| 2 |

故答案为:30、20.
点评:本题考查了一次函数的应用,从图象得到相关信息是解题的关键.

练习册系列答案
相关题目
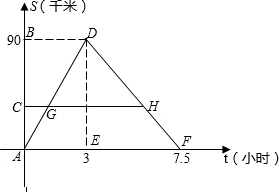
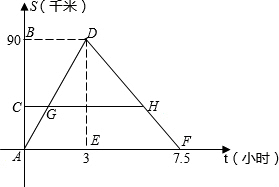 某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:
某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题: