题目内容
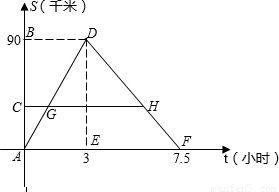
某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题: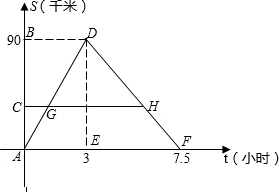
(1)船只从码头A→B,航行的速度为
(2)过点C作CH∥t轴,分别交AD、DF于点G、H,设AC=x,GH=y,求出y与x之间的函数关系式;
(3)若旅游码头C设在离A码头30千米处,一旅游团队在旅游码头C分两组行动,一组乘橡皮艇漂流而下,另一组乘船到达码头B后,立即返回.
①求船只往返C、B两处所用的时间;
②两组在途中相遇,求相遇时船只离旅游码头C有多远.
分析:(1)时间可从图象直接获得,解题时要根据速度=路程÷时间;
(2)因为CH∥t轴,到CH的距离为90-x,所以可用等比性质列出等式,整理即可得到y与x的关系式.
(3)代入函数值30千米即可求出自变量t的值.可以先求出水速,再求出船到B码头的时间和返回时与漂流而下的橡皮艇相遇的时间,时间已得,与水速相乘就是船只离拍摄中心C的距离.
(2)因为CH∥t轴,到CH的距离为90-x,所以可用等比性质列出等式,整理即可得到y与x的关系式.
(3)代入函数值30千米即可求出自变量t的值.可以先求出水速,再求出船到B码头的时间和返回时与漂流而下的橡皮艇相遇的时间,时间已得,与水速相乘就是船只离拍摄中心C的距离.
解答:解:(1)船只从码头A→B,航行的速度为:90÷3=30;
船只从码头B→A,航行的速度为:90÷(7.5-3)=20;
(2)设CH交DE于M,ME=AC=x,DM=90-x

∵GH∥AF,
∴△DGH∽△DAF,
∴
=
,即
=
,
∴y=7.5-
x,
∴y=
-
x,
∴y与x之间的函数关系式y=
-
x;
(3)①当x=30时,y=
-
×30=5(小时).
②设船在静水中的速度是a千米∕时,水流的速度是b千米∕时,即解得即水流的速度是5千米∕时.
根据题意得:
,
解得:
,
则到B码头的时间t1=
=2小时,此时橡皮艇漂流了10千米.
设船又过t2小时与漂流而下橡皮艇相遇.
则(5+20)t2=90-30-10,
∴t2=2.
∴船只离拍摄中心C距离S=(t1+t2)×5=20千米.
答:相遇时船只离旅游码头C有20千米.
船只从码头B→A,航行的速度为:90÷(7.5-3)=20;
(2)设CH交DE于M,ME=AC=x,DM=90-x

∵GH∥AF,
∴△DGH∽△DAF,
∴
| GH |
| AF |
| DM |
| DE |
| y |
| 7.5 |
| 90-x |
| 90 |
∴y=7.5-
| 7.5 |
| 90 |
∴y=
| 15 |
| 2 |
| 1 |
| 12 |
∴y与x之间的函数关系式y=
| 15 |
| 2 |
| 1 |
| 12 |
(3)①当x=30时,y=
| 15 |
| 2 |
| 1 |
| 12 |
②设船在静水中的速度是a千米∕时,水流的速度是b千米∕时,即解得即水流的速度是5千米∕时.
根据题意得:
|
解得:
|
则到B码头的时间t1=
| 90-30 |
| 30 |
设船又过t2小时与漂流而下橡皮艇相遇.
则(5+20)t2=90-30-10,
∴t2=2.
∴船只离拍摄中心C距离S=(t1+t2)×5=20千米.
答:相遇时船只离旅游码头C有20千米.
点评:考查了一次函数的应用,本题难度较大,仔细审题,理清题中各种量之间内在关系,并列出其表达式,题目也就迎刃而解了.另外,与几何相结合也是本题的特点之一.

练习册系列答案
相关题目
 某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:
某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题: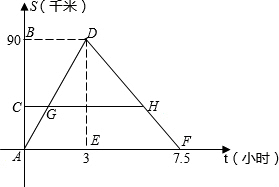 某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:
某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题: