��Ŀ����
����Ŀ������������ˮƽ�½�������ȫ���Ĺ㷺��ע��Ϊ�˽�ij�г��б�ҵ�꼶5 000��ѧ����������������Ǵ��г�ȡ��һ����ѧ����������Ϊ�����������ݴ������õ����µIJ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
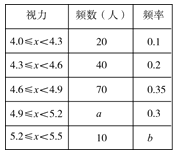
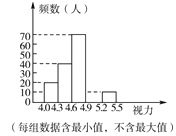
���������ͼ����Ϣ�ش��������⣺
��1����Ƶ���ֲ����У�a=________,b=________��
��2����ȫ����ͳ��ͼ��
��3����������4.6���ϣ���4.6����������������������Ϣ����ȫ�����б�ҵ��������������ѧ���ж��٣�
���𰸡� 60 0.05
��������
��1����Ƶ���ֲ������ڵ���Ϣ��֪��������4.0��x��4.3������Ϊ20��Ƶ��Ϊ0.1���ɴ˼��ɵõ�������ѧ������Ϊ��20��0.1=200���ˣ���������200��0.3�ɵ�a����10��200�ɵ�b��
��2�����ݣ�1������a��ֵ��������ͳ��ͼ�����������ɣ�
��3���������⽫������4.6�����ϵ��������ݵ�Ƶ����ӣ��ٽ����õĺ���5000��˼��ɵõ������ֵ.
��1����Ƶ���ֲ���֪��������4.0��x��4.3������Ϊ20��Ƶ��Ϊ0.1��
���˴ε����������Ϊ20��0.1=200��
��a=200��0.3=60��b=10��200=0.05��
��2���ɣ�1����֪a=60����ȫ����ͳ��ͼ���£�
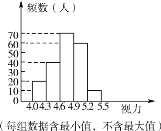
��3��������ɵ���5 000(0.35+0.3+0.05)=3500���ˣ�.
�𣺹���ȫ�о��꼶ѧ����������������3500��.

����Ŀ������Ϊ20cm����Ϊ8cm�ij����ΰ�ֽ������ͼ��ʾ�ķ�ʽճ��������ճ�ϲ��ֵĿ�Ϊ3cm.

(1)�������⣬������ı�������.
��ֽ����x(��) | 1 | 2 | 3 | 4 | 5 | �� |
ֽ���ܳ���y(cm) | 20 | 54 | 71 | �� |
��2��ֱ��д��y��x�Ĺ�ϵʽ.
(3��Ҫʹճ�Ϻ�ij����������Ϊ1656cm2�������ö����������İ�ֽ?