题目内容
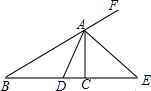如图，AD平分∠BAC，AE是△ABC的外角平分线，交BC延长线于E，且∠BAD=20°，∠E=30°，求∠ADC的度数．
解：∵AD平分∠BAC，∠BAD=20°，
∴∠DAC=∠BAD=20°，∠BAC=2∠BAD=40°，
∴∠FAC=180°-∠BAC=140°，
∵AE是△ABC的外角平分线，
∴∠CAE=
∠FAC=70°，
∵∠E=30°，
∴∠ACE=180°-70°-30°=80°，
∵∠ACE是△ADC的外角，
∴∠ADC=∠ACE-∠DAC=80°-20=60°．
分析：先根据角平分线的性质得出∠DAC的度数，再根据三角形外角的性质求出∠FAC的度数，进而得出∠CAE的度数，根据三角形内角和定理求出∠ACE的度数，由三角形外角的性质即可得出结论．
点评：本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键．
∴∠DAC=∠BAD=20°，∠BAC=2∠BAD=40°，
∴∠FAC=180°-∠BAC=140°，
∵AE是△ABC的外角平分线，
∴∠CAE=
∠FAC=70°，∵∠E=30°，
∴∠ACE=180°-70°-30°=80°，
∵∠ACE是△ADC的外角，
∴∠ADC=∠ACE-∠DAC=80°-20=60°．
分析：先根据角平分线的性质得出∠DAC的度数，再根据三角形外角的性质求出∠FAC的度数，进而得出∠CAE的度数，根据三角形内角和定理求出∠ACE的度数，由三角形外角的性质即可得出结论．
点评：本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，AB平分∠CAD，E为AB上一点，若AC=AD，则下列结论错误的是（ ）
如图，AD为△ABC的角平分线，M为BC的中点，ME∥AD交BA的延长线于E，交AC于F．求证：BE=CF=
如图，AD是△ABC的角平分线，过点D作直线DF∥BA，交△ABC的外角平分线AF于点F，DF与AC交于点E．
