Question

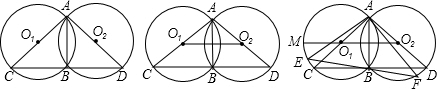
如图，AD和AC分别是⊙O的直径和弦，且∠CAD=30°，OB⊥AC，连接BD．
（1）求证：CB=AB；
（2）若BD=5，求AD的长．

Answer 1

（1）证明：∵OB⊥AC，OB经过圆心，
∴CB=AB；

（2）解：连接CD，设⊙O的半径为r；
∵AD是⊙O的直径，
∴∠ACD=90°；
∵∠CAD=30°，
∴CD=AD=r，AC=r；
∴BC=r；
在Rt△BCD中，r²+r²=25，r=；
∴AD的长为．
分析：（1）由于OB经过圆心且垂直于弦AC，由垂径定理即可得到所求的结论；
（2）此题要通过构建直角三角形求解；连接CD，由圆周角定理知∠ACD=90°；可分别在Rt△ACD和Rt△AOB中，用⊙O的半径表示出CD、AB（即BC）的长，然后在Rt△BCD中，由勾股定理求得⊙O的半径，即可得到AD的长．
点评：此题主要考查的是圆周角定理、垂径定理及勾股定理的综合应用能力．