题目内容
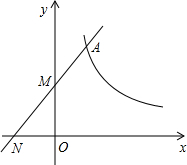
(1)直线y=kx+
与反比例函数y=
(x>0)的图象交于点A,与坐标轴分别交于M、N两点,当AM=MN时,求k的值.
(2)某校为了进一步开展“阳光体育”活动,计划用2000元购买乒乓球拍,用2800元购买羽毛球拍.已知一副羽毛球拍比一副乒乓球拍贵14元.该校购买的乒乓球拍与羽毛球拍的数量能相同吗?请说明理由.
| 2 |
2
| ||
| x |

(2)某校为了进一步开展“阳光体育”活动,计划用2000元购买乒乓球拍,用2800元购买羽毛球拍.已知一副羽毛球拍比一副乒乓球拍贵14元.该校购买的乒乓球拍与羽毛球拍的数量能相同吗?请说明理由.
分析:(1)过点A作AB⊥x轴,垂足为B,首先求出OM的长,再求出A点的坐标,最后代入直线解析式求出k的值;
(2)假设能相等,设兵乓球拍每副x元,则羽毛球拍每副(x+14)元,列出分式方程,解出x的值,然后计算2000÷x是不是一个整数.
(2)假设能相等,设兵乓球拍每副x元,则羽毛球拍每副(x+14)元,列出分式方程,解出x的值,然后计算2000÷x是不是一个整数.
解答: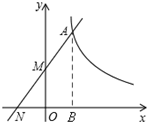 (1)解:过点A作AB⊥x轴,垂足为B.
(1)解:过点A作AB⊥x轴,垂足为B.
对于直线y=kx+
,当x=0 时,y=
,即OM=
.
∵AM=MN,OM∥AB,
∴OM为△ABN的中位线.
∴AB=2OM=2
.将y=2
代入y=
中得 x=1,
∴A(1,2
).
∵点A在直线y=kx+
上,
∴2
=k+
.
∴k=
.
(2)解:不能相同.
理由:假设能相等,设兵乓球拍每副x元,则羽毛球拍每副(x+14)元.
根据题意可列方程
=
,
解得x=35.
但是当x=35时,2000÷35不是一个整数,这不符合实际情况,所以不可能.
 (1)解:过点A作AB⊥x轴,垂足为B.
(1)解:过点A作AB⊥x轴,垂足为B.对于直线y=kx+
| 2 |
| 2 |
| 2 |
∵AM=MN,OM∥AB,
∴OM为△ABN的中位线.
∴AB=2OM=2
| 2 |
| 2 |
2
| ||
| x |
∴A(1,2
| 2 |
∵点A在直线y=kx+
| 2 |
∴2
| 2 |
| 2 |
∴k=
| 2 |
(2)解:不能相同.
理由:假设能相等,设兵乓球拍每副x元,则羽毛球拍每副(x+14)元.
根据题意可列方程
| 2000 |
| x |
| 2800 |
| x+14 |
解得x=35.
但是当x=35时,2000÷35不是一个整数,这不符合实际情况,所以不可能.
点评:本题主要考查反比例函数综合题和分式方程运用的知识点,解答本题的关键是熟练掌握反比例函数的性质以及运用分式方程解决实际问题等知识,此题难度不大.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 已知如图示直线y=kx+b与反比例函数
已知如图示直线y=kx+b与反比例函数 如图,设直线y=kx(k<0)与双曲线y=-
如图,设直线y=kx(k<0)与双曲线y=-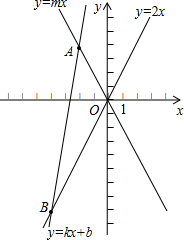 已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).