Question

如图，四边形OABC是平行四边形，以O为圆心，OA为半径的圆交AB于D，延长AO交⊙O于E，连接CD，CE，若CE是⊙O的切线，解答下列问题：

（1）求证：CD是⊙O的切线；

（2）若BC=3，CD=4，求平行四边形OABC的面积．

Answer 1

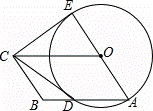
（1）证明：连接OD，

∵OD=OA，

∴∠ODA=∠A，

∵四边形OABC是平行四边形，

∴OC∥AB，

∴∠EOC=∠A，∠COD=∠ODA，

∴∠EOC=∠DOC，

在△EOC和△DOC中

∴△EOC≌△DOC（SAS），

∴∠ODC=∠OEC=90°，

即OD⊥DC，

∴CD是⊙O的切线；

（2）解：∵△EOC≌△DOC，

∴CE=CD=4，

∵四边形OABC是平行四边形，

∴OA=BC=3，

∴平行四边形OABC的面积S=OA×CE=3×4=12．