题目内容
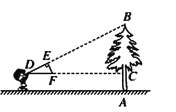
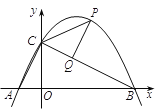
【题目】如图,二次函数y=ax2+bx+2![]() 的图像与y轴交于C点,交x轴于点A(-2,0),B(6,0).
的图像与y轴交于C点,交x轴于点A(-2,0),B(6,0).
⑴ 求该二次函数的表达式;
⑵ P是该函数在第一象限内图像上的动点,过点P作PQ⊥BC于点Q,连接PC、AC.
① 求线段PQ的最大值;
② 若以点P、C、Q为顶点的三角形与△ACO相似,求P点的坐标.
【答案】(1)![]() ;(2)①PQ的最大值=
;(2)①PQ的最大值= ![]() ,② P点的坐标为:P1(4,2
,② P点的坐标为:P1(4,2![]() ),P2
),P2 ![]()
【解析】分析:(1)把点A,B的坐标代入到二次函数的解析式中求解;(2)过点P作PD⊥x轴于点N交BC于点M,P点坐标为![]() ,用t表示出点M,根据二次函数的性质求PM的最大值,再结合三角形相似求PQ的最大值;(3)分两种情况画出图形,根据平行线或相似三角形求解.
,用t表示出点M,根据二次函数的性质求PM的最大值,再结合三角形相似求PQ的最大值;(3)分两种情况画出图形,根据平行线或相似三角形求解.
详解:⑴∵y=ax2+bx+![]() 的图像过点A(-2,0),B(6,0).
的图像过点A(-2,0),B(6,0).
∴![]() 解之得:
解之得: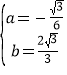 ;
;
∴所求二次函数的表达式为:![]() .
.
⑵①设P点坐标为:![]() ,且0<t<6,
,且0<t<6,
令x=0,则y=4,∴C(0,2![]() ).
).
设BC的表达式为:
y=mx+n(m≠0)过B(6,0),C(0,![]() ),
),
![]() ,解之得:
,解之得: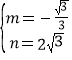 ,∴BC的表达式为:
,∴BC的表达式为:![]() ,
,
过点P作PD⊥x轴于点N交BC于点M,(如图1)
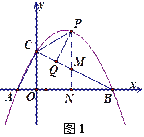
∴点M的横坐标为t,∴它的纵坐标为![]() ,
,
∴M![]() .
.
PM=yP-yM=![]() ,
,
∵x轴⊥y轴,PQ⊥BC,PD⊥x轴.
∴∠AOC=∠COB=∠CQP=∠PQM=∠MDB=90°,
又∵AO=2,OB=8,CO=4,
∴![]() ,∴△OAC∽△OCB,∴∠ACO=∠CBO=∠MPQ,
,∴△OAC∽△OCB,∴∠ACO=∠CBO=∠MPQ,
∴△OAC∽△OCB∽△DMB∽△QMP.
∵![]() ,
,
∴cos∠MPQ=cos∠ACO=![]() .
.
∵cos∠MPQ=![]() ,
,
∴![]() .
.
∵a<0,且t=3的值在0<t<6的范围内,
∴当t=3时,PQ的最大值=![]() .
.
②(ⅰ)当△QPC∽△OAC时,(如图2)
则∠ACO=∠CBA=∠PCQ,
∴PC∥x轴,
由抛物线的对称性知:点C与点P关于抛物线的对称轴对称,
∴P点的坐标为(4,![]() ).
).
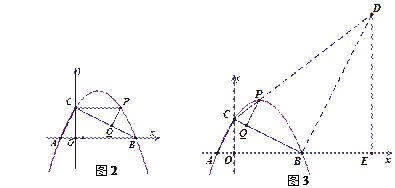
(ⅱ)当△QCP∽△OAC时,(如图3)
则∠CAO=∠PCQ,
∴tan∠CAO=tan∠PCQ,
过点B作BD⊥BC交CP的延长线于点D,
再过点D作DE⊥x轴于点E,
则△OBC∽△EDB,
∴![]() ,
,
∴BE=![]() CO=
CO=![]() ×2
×2![]() =6,∴OE=OB+BE=12,
=6,∴OE=OB+BE=12,
DE=![]() BO=
BO=![]() ×6=6
×6=6![]() ,∴点D的坐标为(12,6
,∴点D的坐标为(12,6![]() ).
).
设直线CD的表达式为y=ex+f,且过点C(0,![]() ),D(12,6
),D(12,6![]() ),
),
∴![]() ,解得,
,解得,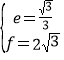 .
.
∴直线CD的表达式为:![]() ,
,
∴P坐标是方程组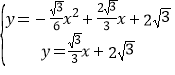 的解,
的解,
解之得: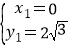 (舍),
(舍),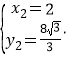
∴点P的坐标为(![]() ).
).
综上所述:P点的坐标为:P1(4,![]() ),P2(
),P2(![]() ).
).