题目内容
如图,抛物线 经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,
经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0, ),⊙P的圆心P在y轴上,且经过B、C两点.
),⊙P的圆心P在y轴上,且经过B、C两点.(1)求抛物线的解析式;
(2)D在抛物线上,且C、D两点关于抛物线的对称轴对称,问直线BD是否经过圆心P?并说明理由;
(3)设直线BD交⊙P于另一点E,求经过点E和⊙P的切线的解析式.

【答案】分析:(1)将点C的坐标代入抛物线解析式即可求得c的值;
(2)已知D点坐标,可求直线BD的解析式,连接BP,设⊙P的半径为r,求出r,OP的值即可.
(3)过点E作EF⊥y轴于F,可求得△OPB≌△FPE,求出点P的坐标.然后由射影定理求得PE2=PF•PN,根据此关系式求解.
解答:解:(1)∵抛物线 经过点C(0,
经过点C(0, ),
),
∴c= ,
,
∴该抛物线的解析式为 -
- ;
;
(2)∵抛物线的解析式为 -
- ,
,
∴对称轴为x=- =-
=- .
.
又∵C(0, ),C、D两点关于抛物线的对称轴对称,
),C、D两点关于抛物线的对称轴对称,
∴D(- ,-
,- ).
).
令 x2+
x2+ x-
x- =0,
=0,
解得,x1=- ,x2=
,x2= ,
,
即A(- ,0)、B(
,0)、B( ,0).
,0).
易求直线BD的解析式为:y= x-
x- .
.
设⊙P的半径为r.则在直角△OBP中,根据勾股定理知BP2=OB2+OP2,即r2=( )2+(
)2+( -r)2,
-r)2,
解得,r=1,则OP=OC-r= -1=
-1= .
.
∴P(0, ).
).
点P的坐标满足直线BD的解析式y= x-
x- .即直线BD经过圆心P;
.即直线BD经过圆心P;
(3)过点E作EF⊥y轴于F,得△OPB≌△FPE,则E(- ,-1).
,-1).
设经过E点⊙P的切线l交y轴于点N.
则∠PEN=90°,EF⊥PN,
∴PE2=PF•PN(射影定理),
∴PN=2,N(0,-2.5),(11分)
∴切线l为:y=- x-
x- .
.
点评:本题考查的是二次函数的综合应用.难度较大.解题时,要数形结合,以防将点D的坐标误写为( ,-
,- ).
).
(2)已知D点坐标,可求直线BD的解析式,连接BP,设⊙P的半径为r,求出r,OP的值即可.
(3)过点E作EF⊥y轴于F,可求得△OPB≌△FPE,求出点P的坐标.然后由射影定理求得PE2=PF•PN,根据此关系式求解.
解答:解:(1)∵抛物线
 经过点C(0,
经过点C(0, ),
),∴c=
 ,
,∴该抛物线的解析式为
 -
- ;
;(2)∵抛物线的解析式为
 -
- ,
,∴对称轴为x=-
 =-
=- .
.又∵C(0,
 ),C、D两点关于抛物线的对称轴对称,
),C、D两点关于抛物线的对称轴对称,∴D(-
 ,-
,- ).
).令
 x2+
x2+ x-
x- =0,
=0,解得,x1=-
 ,x2=
,x2= ,
,即A(-
 ,0)、B(
,0)、B( ,0).
,0).
易求直线BD的解析式为:y=
 x-
x- .
.设⊙P的半径为r.则在直角△OBP中,根据勾股定理知BP2=OB2+OP2,即r2=(
 )2+(
)2+( -r)2,
-r)2,解得,r=1,则OP=OC-r=
 -1=
-1= .
.∴P(0,
 ).
).点P的坐标满足直线BD的解析式y=
 x-
x- .即直线BD经过圆心P;
.即直线BD经过圆心P;(3)过点E作EF⊥y轴于F,得△OPB≌△FPE,则E(-
 ,-1).
,-1).设经过E点⊙P的切线l交y轴于点N.
则∠PEN=90°,EF⊥PN,
∴PE2=PF•PN(射影定理),
∴PN=2,N(0,-2.5),(11分)
∴切线l为:y=-
 x-
x- .
.点评:本题考查的是二次函数的综合应用.难度较大.解题时,要数形结合,以防将点D的坐标误写为(
 ,-
,- ).
). 
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
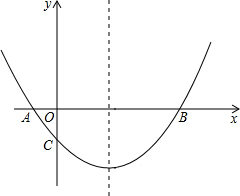 (2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,
(2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0, 如图,抛物线经过A(4,0)、B(1,0)、C(0,-2)三点.
如图,抛物线经过A(4,0)、B(1,0)、C(0,-2)三点. A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C.
A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C. 经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,
经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0, ),⊙P的圆心P在y轴上,且经过B、C两点.
),⊙P的圆心P在y轴上,且经过B、C两点.