题目内容
【题目】已知![]() 为
为![]() 直径,
直径,![]() 是直径
是直径![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() ,
,![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 上一点(不与点
上一点(不与点![]() ,
,![]() 重合),且
重合),且![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() .
.
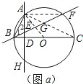
![]() 如图
如图![]() ,当点
,当点![]() 在线段
在线段![]() 上时,试判断
上时,试判断![]() 与
与![]() 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;
![]() 当点
当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,其它条件不变.
时,其它条件不变.

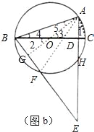
①请你在图![]() 中画出符合要求的图形,并参照图
中画出符合要求的图形,并参照图![]() 标记字母;
标记字母;
②判断![]() 中的结论是否还成立,请说明理由.
中的结论是否还成立,请说明理由.
【答案】见解析
【解析】
(1)AE=BE,可根据垂径定理得出弧AB=弧BH,已知了弧AB=弧AF,因此弧BH=弧AF,根据圆周角定理可得出∠BAH=∠ABF根据等角对等边即可得出AE=BE.(方法不唯一)
(2)结论不变,证法同(1),根据垂径定理可得出弧AC=弧CH,因此弧AB=弧BH,由于弧AB=弧AF,因此弧AF=弧BH,即∠BAE=∠ABE,因此AE=BE.
![]()
证法①:
∵![]() 为
为![]() 直径,
直径,![]() 于点
于点![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]() .
.
证法②:
连![]() ,
,![]()
∵![]() 是
是![]() 直径,
直径,![]() 于点
于点![]()
∴![]()
∴![]() ,
,![]()
∴![]()
∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]() .
.
证法③:
连接![]() ,交
,交![]() 于点
于点![]()
∵![]()
∴![]()
又∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()

![]() ①所画图形如图所示,
①所画图形如图所示,![]() 成立
成立
证法①:
∵![]() 是
是![]() 直径,
直径,![]() 于点
于点![]()
∴![]()
又![]()
∴![]()
∴![]()
∴![]() .
.
证法②:
连接![]() ,
,![]()
∵![]() 是
是![]() 直径,
直径,![]() 于点
于点![]()
∴![]()
∵![]()
∴![]()
又∵![]()
∴![]()
又∵![]()
∴![]()
∴![]() .
.
证法③:
连接![]() 并延长
并延长![]() 交
交![]() 于点
于点![]()
∵![]() ,
,![]() 过圆心
过圆心
∴![]()
又∵![]() 于点
于点![]()
∴![]()
又∵![]() 为
为![]() 直径,
直径,![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]() .
.

练习册系列答案
相关题目





