题目内容

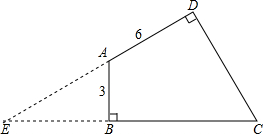
在四边形ABCD中，∠B=∠D=90°，∠A=120°，AB=3，AD=6，延长DA，CB相交于点E．
①求Rt△DCE的面积；　　
②求四边形ABCD的面积．

解：①∵∠B=∠D=90°，∠A=120°，
∴∠C=360°-90°×2-120°=60°，
∴∠E=90°-60°=30°，
∵AB=3，
∴AE=2AB=2×3=6，
∴DE=AE+AD=6+6=12，
在Rt△DEC中，CD=DEtan∠E=12×tan30°=4 $\text{[math]}$ ，
∴Rt△DCE的面积= $\text{[math]}$ ×12×4 $\text{[math]}$ =24 $\text{[math]}$ ；

②在Rt△ABE中，BE= $\text{[math]}$ =3 $\text{[math]}$ ，
四边形ABCD的面积=△DEC的面积-△ABE的面积，
=24 $\text{[math]}$ - $\text{[math]}$ ×3 $\text{[math]}$ ×3
= $\text{[math]}$ ．
分析：①根据四边形的内角和等于360°求出∠C，再根据直角三角形两锐角互余求出∠E=30°，然后根据直角三角形30°角所对的直角边等于斜边的一半求出AE=6，再求出DE的长，然后解直角三角形求出CD，然后根据三角形的面积公式列式进行计算即可得解；
②先解直角三角形求出BE，再根据四边形ABCD的面积=△DEC的面积-△ABE的面积列式进行计算即可得解．
点评：本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质，勾股定理的应用，以及四边形的内角和等于360°，熟记性质是解题的关键．