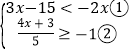题目内容
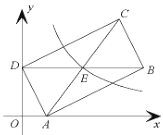
【题目】已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为边
为边![]() 上任意一点,连结
上任意一点,连结![]() ,
,![]() ,以
,以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() ,
,![]() .
.

(1)若点![]() 为
为![]() 的中点,证明:
的中点,证明:![]() .
.
(2)若![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长.
的长.
(3)作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .
.
①当点![]() 落在线段
落在线段![]() 上时,设线段
上时,设线段![]() ,
,![]() 交于点
交于点![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
②在点![]() 的运动过程中,当点
的运动过程中,当点![]() 落在四边形
落在四边形![]() 内时(不包括边界),则
内时(不包括边界),则![]() 的范围是________(直接写出答案).
的范围是________(直接写出答案).
【答案】(1)证明见解析;(2)4或5或6;(3)①6:5;②![]() .
.
【解析】
(1)由![]() 为
为![]() 直径,可得
直径,可得![]() ,由点
,由点![]() 为
为![]() 的中点,可得
的中点,可得![]() ,据此证明
,据此证明![]() ,可得
,可得![]() .
.
(2)![]() 为等腰三角形,需要分类讨论:①
为等腰三角形,需要分类讨论:①![]() ,②
,②![]() ,③
,③![]() ,综合三种情况可得
,综合三种情况可得![]() 的长.
的长.
(3)①![]() 与
与![]() 的高相等,面积之比等于底之比;连接
的高相等,面积之比等于底之比;连接![]() ,证明
,证明![]() ∥
∥![]() ,再利用相似三角形性质易求得
,再利用相似三角形性质易求得![]() 与
与![]() 的面积之比.
的面积之比.
②当点![]() 落在矩形
落在矩形![]() 对角线
对角线![]() 上时,通过证明
上时,通过证明![]() ,可得
,可得![]() 长,即可得
长,即可得![]() 的最小值,最大值很容易看出为10.
的最小值,最大值很容易看出为10.
(1)∵![]() 为
为![]() 直径,∴
直径,∴![]() ,
,
∵点![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
在![]() 和
和![]() 中,
中,
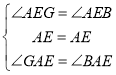
∴![]() ,
,
∴![]() .
.
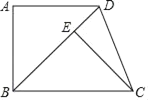
(2)如图1,![]() 为等腰三角形,分三种情况:
为等腰三角形,分三种情况:
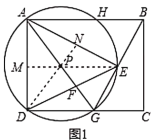
①![]() 时,
时,
∵![]() 为
为![]() 直径,∴
直径,∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,
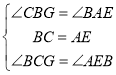
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
②![]() 时,如图,过点E作EM⊥AD于M,
时,如图,过点E作EM⊥AD于M,
∵![]() ,EM⊥AD,∴
,EM⊥AD,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即点
,即点![]() 为
为![]() 的中点,
的中点,
∴由(1)得![]() ,
,
∴![]() .
.
③当![]() 时,如图,过点D作DN⊥AE于N,
时,如图,过点D作DN⊥AE于N,
∵![]() ,DN⊥AE,∴
,DN⊥AE,∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
∴![]() ,
,
综上所述,![]() 或5或6.
或5或6.
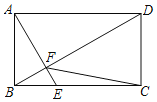
(3)①如图2,点![]() 与
与![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() ,连接
,连接![]() ,
,
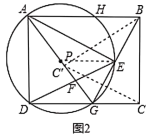
由轴对称性质得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]()
∴在![]() 和
和![]() 中,
中,
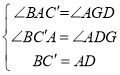
∴![]()
∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵AE⊥BG,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() 与
与![]() 的面积之比为
的面积之比为![]() .
.
②如图3,

当点![]() 落在矩形
落在矩形![]() 对角线
对角线![]() 上时,
上时,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴ ![]() ,即
,即![]() ,
,
∴![]() ,
,
则当点![]() 向右运动且不与点
向右运动且不与点![]() 重合时,
重合时,![]() 始终落在四边形
始终落在四边形![]() 内部,
内部,
∴![]() ,
,
故答案为:![]() .
.

【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
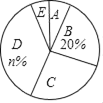
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)郑州市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?