题目内容
己知:直线AB:y=2x+8与x、y轴交于A、B两点,
(1)若C为x轴上一点,且△ABC面积为32,求C点坐标;
(2)若过C点的直线l与直线y=2x+8的夹角为45°,求直线l的解析式.
(1)若C为x轴上一点,且△ABC面积为32,求C点坐标;
(2)若过C点的直线l与直线y=2x+8的夹角为45°,求直线l的解析式.
解:(1)根据题意画出图形: 则可知A和B的坐标分别为:A(﹣4,0),B(0,8),
∵S△ABC= OB·AC=32
OB·AC=32
∴AC=8,
设C(x,0),则AC=|x﹣(﹣4)|=8,
∴x=4或﹣12,
故C点的坐标为:(4,0)或(﹣12,0).
(2)①当直线l过点C(4,0)时, 过点C作CD⊥AB于点D,然后在直线AB上截取DE1=DE2=CD,
则D点的坐标为(﹣ ,
, ),CD=
),CD= ,
,
根据两点之间的距离公式可求出点E1和E2的坐标分别为:( ,
, )和(﹣
)和(﹣ ,﹣
,﹣ )
)
则直线CE1和CE2为所求的直线l,其解析式分别为:y=﹣3x+12和y= ;
;
②当直线l过点C(﹣12,0)时,
同理,此时D点坐标为(﹣ ,﹣
,﹣ ),CD=
),CD= ,
,
点E3和E4的坐标分别为:(﹣ ,
, )和(﹣
)和(﹣ ,﹣
,﹣ )
)
则直线CE3和CE4为所求的直线l,其解析式分别为:y= 和y=﹣3x﹣36.
和y=﹣3x﹣36.

∵S△ABC=
 OB·AC=32
OB·AC=32∴AC=8,
设C(x,0),则AC=|x﹣(﹣4)|=8,
∴x=4或﹣12,
故C点的坐标为:(4,0)或(﹣12,0).
(2)①当直线l过点C(4,0)时, 过点C作CD⊥AB于点D,然后在直线AB上截取DE1=DE2=CD,
则D点的坐标为(﹣
 ,
, ),CD=
),CD= ,
,根据两点之间的距离公式可求出点E1和E2的坐标分别为:(
 ,
, )和(﹣
)和(﹣ ,﹣
,﹣ )
)则直线CE1和CE2为所求的直线l,其解析式分别为:y=﹣3x+12和y=
 ;
;②当直线l过点C(﹣12,0)时,
同理,此时D点坐标为(﹣
 ,﹣
,﹣ ),CD=
),CD= ,
,点E3和E4的坐标分别为:(﹣
 ,
, )和(﹣
)和(﹣ ,﹣
,﹣ )
)则直线CE3和CE4为所求的直线l,其解析式分别为:y=
 和y=﹣3x﹣36.
和y=﹣3x﹣36.

练习册系列答案
相关题目

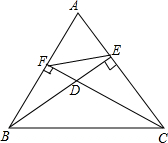 (2012•嘉定区一模)己知BE、CF分别是△ABC的边AC、AB上的高,高BE、CF所在的直线相交于点D(如图)
(2012•嘉定区一模)己知BE、CF分别是△ABC的边AC、AB上的高,高BE、CF所在的直线相交于点D(如图)