题目内容
6.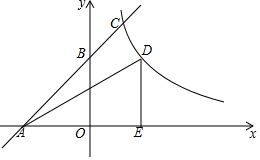 在平面直角坐标系内,点O为坐标原点,直线y=x+4交x轴于点A,交y轴于点B,点C(2,m)在直线y=x+4上,反比例函数
在平面直角坐标系内,点O为坐标原点,直线y=x+4交x轴于点A,交y轴于点B,点C(2,m)在直线y=x+4上,反比例函数y=$\frac{n}{x}$经过点C.
(1)求m,n的值;
(2)点D在反比例函数y=$\frac{n}{x}$的图象上,过点D作X轴的垂线,点E为垂足,若OE=3,连接AD,求tan∠DAE的值.
分析 (1)把点C的坐标代入直线y=x+4,求出m,得到点C的坐标,代入反比例函数解析式,计算即可;
(2)分别求出DE、AE的长,根据正切的定义计算即可.
解答 解:(1)∵点C(2,m)在直线y=x+4上,
∴m=2+4=6,
∴点C的坐标为(2,6),
把x=2,y=6代入y=$\frac{n}{x}$,
得6=$\frac{n}{2}$,
解得,n=12;
(2)∵OE=3,DE⊥x轴,
∴点D的横坐标是3,
当x=3时,y=$\frac{12}{3}$=4,
∴点D的坐标为(3,4),
∴DE=4,
把y=0代入y=x+4,
得,x=-4,即OA=4,
∴AE=7,
∴tan∠DAE=$\frac{DE}{AE}$=$\frac{4}{7}$.
点评 本题考查的是反比例函数与一次函数的交点问题,掌握函数图象上点的坐标特征、锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
14. 如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是( )
如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是( )
 如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是( )
如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是( )| A. | 0 | B. | 7 | C. | 快 | D. | 乐 |
18.已知反比例函数y=$\frac{k}{x}$(k≠0)的图象在其所在现象内,y的值随x的值的增大而增大,则反比例函数y=$\frac{k}{x}$的图象在( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
16.农业部门引进一批新麦种,在播种前做了五次发芽试验,目的是想了解一粒这样的麦种发芽情况,实验统计数据如下:
估计在与实验条件相同的情况下,种一粒这样的麦种发芽的概率约为0.98.
| 实验的麦种数/粒 | 500 | 500 | 500 | 500 | 500 |
| 发芽的麦种数/粒 | 492 | 487 | 491 | 493 | 489 |
| 发芽率/% | 98.40 | 97.40 | 98.20 | 98.60 | 97.80 |
 如图,在等边三角形ABC中,AB=2,点D为BC的中点,DE∥AB交AC于点E,过点E作EF⊥DE,交BC的延长线于点F,则图中长度为1的线段有( )
如图,在等边三角形ABC中,AB=2,点D为BC的中点,DE∥AB交AC于点E,过点E作EF⊥DE,交BC的延长线于点F,则图中长度为1的线段有( ) 如图是由5个大小相同的小立方体组成的立体图形,这个立体图形的俯视图是( )
如图是由5个大小相同的小立方体组成的立体图形,这个立体图形的俯视图是( )


