题目内容
平面直角坐标系中,已知点O(0,0)、A(0,2)、B(1,0),点P是反比例函数 图象上的一个动点,过点P作PQ⊥x轴,垂足为点Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有 ( )
图象上的一个动点,过点P作PQ⊥x轴,垂足为点Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有 ( )| A.1个 | B.2个 | C.3个 | D.4个 |
D解析:
∵点P是反比例函数y=﹣ 图象上,
图象上,
∴设点P(x,y),
当△PQO∽△AOB时,则 ,
,
又PQ=y,OQ=﹣x,OA=2,OB=1,
即 ,即y=﹣2x,
,即y=﹣2x,
∵xy=﹣1,即﹣2x2=﹣1,
∴x=± ,
,
∴点P为( ,﹣
,﹣ )或(﹣
)或(﹣ ,
, );
);
同理,当△PQO∽△BOA时,
求得P(﹣ ,
, )或(
)或( ,﹣
,﹣ );
);
故相应的点P共有4个.
故选D.

∵点P是反比例函数y=﹣
 图象上,
图象上,∴设点P(x,y),
当△PQO∽△AOB时,则
 ,
,又PQ=y,OQ=﹣x,OA=2,OB=1,
即
 ,即y=﹣2x,
,即y=﹣2x,∵xy=﹣1,即﹣2x2=﹣1,
∴x=±
 ,
,∴点P为(
 ,﹣
,﹣ )或(﹣
)或(﹣ ,
, );
);同理,当△PQO∽△BOA时,
求得P(﹣
 ,
, )或(
)或( ,﹣
,﹣ );
);故相应的点P共有4个.
故选D.


练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B.
一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B. 21、如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
21、如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.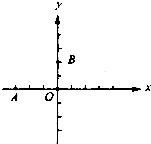 18、如图,在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是O(0,0),A(-3,0),B(0,2),求平行四边形第四个顶点C的坐标.
18、如图,在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是O(0,0),A(-3,0),B(0,2),求平行四边形第四个顶点C的坐标. 出M在抛物线内部(指抛物线与X轴所围成的部分)时t的取值范围.
出M在抛物线内部(指抛物线与X轴所围成的部分)时t的取值范围.