题目内容
如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.
 (1)快艇从港口B到小岛C需要多长时间?
(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.

解:(1)∵∠CBO=60°,∠COB=30°,
∴∠BCO=90°.
在Rt△BCO中,∵OB=120,
∴BC= OB=60,
OB=60,
∴快艇从港口B到小岛C的时间为:60÷60=1(小时);
(2)过C作CD⊥OA,垂足为D,设相会处为点E.
则OC=OB•cos30°=60 ,CD=
,CD= OC=30
OC=30 ,OD=OC•cos30°=90,
,OD=OC•cos30°=90,
∴DE=90﹣3v.
∵CE=60,CD2+DE2=CE2,
∴(30 )2+(90﹣3v)2=602,
)2+(90﹣3v)2=602,
∴v=20或40,
∴当v=20km/h时,OE=3×20=60km,
当v=40km/h时,OE=3×40=120km.


练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目


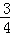 B. m>
B. m>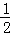 <m<2 D.
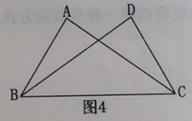
<m<2 D.  (k>0)与边长为3的等边△AOB(O为坐标原点)的边OA、AB分别交于C、D两点,且OC=2BD,则k的值为 .
(k>0)与边长为3的等边△AOB(O为坐标原点)的边OA、AB分别交于C、D两点,且OC=2BD,则k的值为 .

 经过点D(-1,0),
经过点D(-1,0), D(0,-1),E(1,0).
D(0,-1),E(1,0).
 ,点D1与D2是旋转前后的对应点,求图③中抛物线的函数表达式.
,点D1与D2是旋转前后的对应点,求图③中抛物线的函数表达式. 相交于A、B两点,D2与D3是旋转前后如图④,求线段AB的长.
相交于A、B两点,D2与D3是旋转前后如图④,求线段AB的长.