题目内容
由于受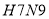 禽流感的影响,我市某城区今年
禽流感的影响,我市某城区今年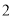 月份鸡的价格比
月份鸡的价格比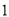 月份下降
月份下降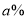 ,
,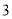 月份比
月份比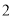 月份下降
月份下降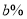 ,已知
,已知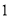 月份鸡的价格为
月份鸡的价格为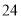 元/千克,设
元/千克,设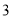 月份鸡的价格为
月份鸡的价格为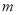 元/千克,则()
元/千克,则()
A.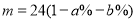 B.
B.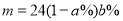
C. 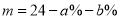 D.
D.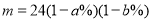
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
题目内容
由于受 禽流感的影响,我市某城区今年
禽流感的影响,我市某城区今年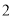 月份鸡的价格比
月份鸡的价格比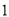 月份下降
月份下降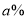 ,
,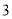 月份比
月份比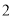 月份下降
月份下降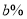 ,已知
,已知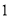 月份鸡的价格为
月份鸡的价格为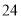 元/千克,设
元/千克,设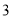 月份鸡的价格为
月份鸡的价格为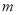 元/千克,则()
元/千克,则()
A.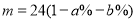 B.
B.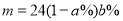
C. 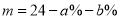 D.
D.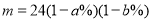
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案