题目内容

4．等腰三角形的两边长分别为5和10，则它的周长为25．

分析 根据腰为5或10，分类求解，注意根据三角形的三边关系进行判断．

解答 解：当等腰三角形的腰为5时，三边为5，5，10，5+5=10，三边关系不成立，
当等腰三角形的腰为10时，三边为5，10，10，三边关系成立，周长为5+10+10=25．
故答案为：25．

点评 本题考查了等腰三角形的性质，三角形三边关系定理．关键是根据已知边那个为腰，分类讨论．

练习册系列答案
相关题目
10．已知函数y=（k-1）${x}^{{k}^{2}-3k+1}$．
（1）当k等于多少时，它是y关于x的正比例函数？
（2）当k是何值时，y是x的反比例函数．
11．足球比赛的计分规则为：胜一场得3分，平一场得1分，负一场得0分．一个队打14场负5场共得19分，那么这个队胜了多少场？
12．如图，抛物线与 轴交于A（6，0）、D （-2，0）两点，与y轴交于点B（0，6），C为顶点．
（1）求抛物线的解析式；
（2）判断△ABC与△BOD是否相似；
（3）作CE⊥y轴于点E，F为y轴上一点（在点E的下方），且tan∠ECF=$\frac{1}{2}$，判断直线CF与△ABC外接圆的位置关系；
（4）在（3）的条件下，若点G为△ABC外接圆上一动点，OP是△FOG中线，求OP的最大值．
19．如图，将△ABC绕点B逆时针旋转90°后得到△A′BC′，则点A的对应点A′的坐标为（2，-3）．
9．某小区为了绿化环境，计划分两次购进A、B两种花草，第一次分别购进A、B两种花草30棵和15棵，共花费675元；第二次分别购进A、B两种花草12棵和5棵．两次共花费940元（两次购进的A、B两种花草价格均分别相同）．
（1）A、B两种花草每棵的价格分别是多少元？
（2）若再次购买A、B两种花草共12棵（A、B两种花草价格不变），且A种花草的数量不少于B种花草的数量的4倍，请你给出一种费用最省的方案，并求出该方案所需费用．
16．如图，圆锥的侧面展开图是半径为3，圆心角为90°的扇形，则该圆锥的底面圆的半径为（　　）
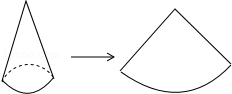
A．$\frac{3}{4}$πB．$\frac{3}{2}$πC．$\frac{3}{4}$D．$\frac{3}{2}$
13．计算：-32×（-2）3的结果是（　　）
A．36B．-36C．-72D．72
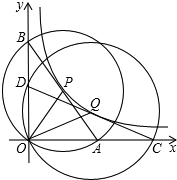14．如图，在平面直角坐标系中，O为坐标原点，P是反比例函数y=$\frac{12}{x}$（x＞0）图象上任意一点，以P为圆心，PO为半径的圆与坐标轴分别交于点A、B；Q是图象上异于点P的另一点，以Q为圆心、QO为半径画圆与坐标轴分别交于点C、D，则线段OA、OB、OC、OD之间的数量关系为OA•OB=OC•OD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网