题目内容
如图,抛物线 经过点A(-1,0)、B(3,0)、C(0,
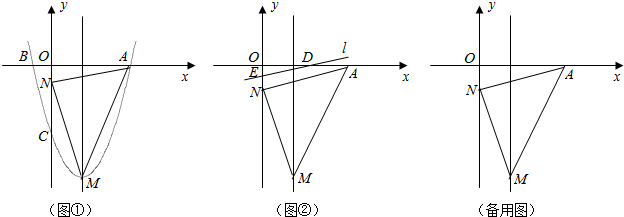
经过点A(-1,0)、B(3,0)、C(0, ),连接AC、BC,将△ABC绕点C逆时针旋转,使点A落在x轴上,得到△DCE,此时,DE所在直线与抛物线交于第一象限的点F.
),连接AC、BC,将△ABC绕点C逆时针旋转,使点A落在x轴上,得到△DCE,此时,DE所在直线与抛物线交于第一象限的点F.
(1)求抛物线 对应的函数关系式.
对应的函数关系式.
(2)求点A所经过的路线长.
(3)抛物线的对称轴上是否存在点P使△PDF是等腰三角形.
若存在,求点P的坐标;若不存在,说明理由.
(1)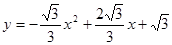 (2)
(2)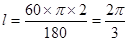 (3)P(1,2),(1,-2),(1,2
(3)P(1,2),(1,-2),(1,2 )或(1,
)或(1,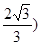
解析试题分析:(1)抛物线 经过点A(-1,0)、B(3,0)、C(0,
经过点A(-1,0)、B(3,0)、C(0, ),那么
),那么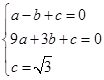 ,解得
,解得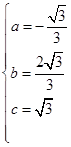 ,所以抛物线
,所以抛物线 对应的函数关系式为
对应的函数关系式为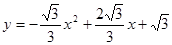
(2)将△ABC绕点C逆时针旋转,使点A落在x轴上,得到△DCE,则D的坐标(1,0)。所以AD=1+1=2,点A(-1,0)、C(0, ),在
),在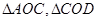 ,
,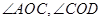 是直角,AO=1,CO=
是直角,AO=1,CO= ,由勾股定理得
,由勾股定理得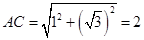 ,同理CD=2,所以三角形ACD是等边三角形,
,同理CD=2,所以三角形ACD是等边三角形,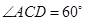 ;点A所经过的路线是一个扇形的弧长,圆心角为
;点A所经过的路线是一个扇形的弧长,圆心角为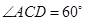 ,半径为AC=2所以扇形的弧长=
,半径为AC=2所以扇形的弧长=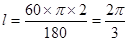
(3)抛物线的对称轴上存在点P使△PDF是等腰三角形,抛物线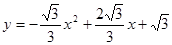 的对称轴
的对称轴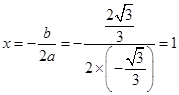 ;设点P的坐标为(1,a),F的坐标为(x,y),则P、D都在抛物线的对称轴上; 假设△PDF是等腰三角形,FD是腰,则PD=FD,由(1)知D的坐标(1,0),所以PD=
;设点P的坐标为(1,a),F的坐标为(x,y),则P、D都在抛物线的对称轴上; 假设△PDF是等腰三角形,FD是腰,则PD=FD,由(1)知D的坐标(1,0),所以PD=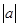 ,FD=
,FD= 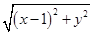 ,则
,则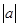 =
=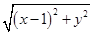 ,而点F在抛物线上,所以F的坐标满足的解析式
,而点F在抛物线上,所以F的坐标满足的解析式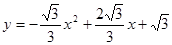 ,解得
,解得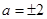 ;当△PDF是等腰三角形,FD是底边,那么PF、PD是腰,所以PF=PD,则PD=
;当△PDF是等腰三角形,FD是底边,那么PF、PD是腰,所以PF=PD,则PD=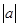 ,F的坐标为(x,y),F的坐标满足的解析式
,F的坐标为(x,y),F的坐标满足的解析式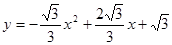 ;PF=
;PF=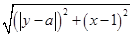 ,则
,则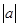 =
=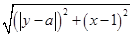 ,解得a=2
,解得a=2 或a=
或a=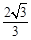 ,所以P点的坐标为P(1,2),(1,-2),(1,2
,所以P点的坐标为P(1,2),(1,-2),(1,2 )或(1,
)或(1,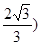
考点:抛物线,等腰三角形
点评:本题考查抛物线,等腰三角形,要求考生会用待定系数法求函数的解析式,掌握抛物线的性质,熟悉等腰三角形的性质

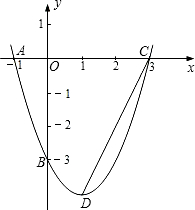 如图,抛物线经过点A(-1,0),B(0,-3),C(3,0)三点,
如图,抛物线经过点A(-1,0),B(0,-3),C(3,0)三点, (2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).
(2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8). 经过点A(1,0),与y轴交于点B。
经过点A(1,0),与y轴交于点B。
 经过点A(1,0),与
经过点A(1,0),与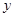 轴交于点B.
轴交于点B.