题目内容
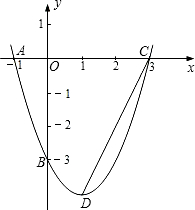如图，抛物线经过点A（-1，0），B（0，-3），C（3，0）三点，（1）求此抛物线的解析式；
（2）若抛物线的顶点为D，求sin∠ACD的值．
分析：（1）已知了抛物线图象上的三点坐标，可利用待定系数法求得该抛物线的解析式．
（2）将所得抛物线的解析式化为顶点坐标式，即可求得点D的坐标，过D作DH⊥x轴于H，根据D、C的坐标，即可得到CH、DH的长，利用勾股定理可求得CD的长，即可在Rt△HCD中求得∠ACD的正弦值．
（2）将所得抛物线的解析式化为顶点坐标式，即可求得点D的坐标，过D作DH⊥x轴于H，根据D、C的坐标，即可得到CH、DH的长，利用勾股定理可求得CD的长，即可在Rt△HCD中求得∠ACD的正弦值．
解答：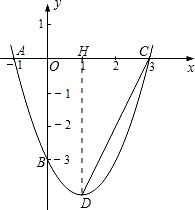
解：（1）设此抛物线的解析式为y=ax2+bx+c；（1分）
∵抛物线经过点A（-1，0），B（0，-3），C（3，0）三点，
∴
∴
；
∴此抛物线的解析式为y=x2-2x-3．（5分）
（2）过点D作DH⊥x轴于H；
由y=x2-2x-3=（x-1）2-4，即D（1，-4）；（7分）
在Rt△DHC中，∠DHC=90°，DH=4，CH=2，
由CH2+DH2=CD2，
∴CD=2
；（8分）
sin∠ACD=
=
=
．（10分）
解：（1）设此抛物线的解析式为y=ax2+bx+c；（1分）∵抛物线经过点A（-1，0），B（0，-3），C（3，0）三点，
∴
|
∴
|
∴此抛物线的解析式为y=x2-2x-3．（5分）
（2）过点D作DH⊥x轴于H；
由y=x2-2x-3=（x-1）2-4，即D（1，-4）；（7分）
在Rt△DHC中，∠DHC=90°，DH=4，CH=2，
由CH2+DH2=CD2，
∴CD=2
| 5 |
sin∠ACD=
| DH |
| CD |
| 4 | ||
2
|
2
| ||
| 5 |
点评：此题主要考查了二次函数解析式的确定、顶点坐标的求法以及解直角三角形等知识，属于基础知识，需要熟练掌握．
练习册系列答案
相关题目
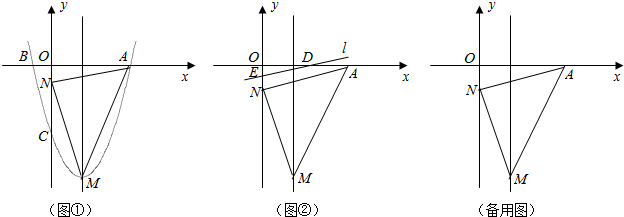
（2013•高要市二模）已知：如图，抛物线经过点O、A、B三点，四边形OABC是直角梯形，其中点A在x轴上，点C在y轴上，BC∥OA，A（12，0）、B（4，8）．
经过点A(1,0)，与y轴交于点B。
经过点A(1，0)，与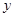
轴交于点B.