题目内容
如图所示，AB∥CD，∠E=27°，∠C=52°，则∠EAB的度数为（ ）
A．25°
B．63°
C．79°
D．101°
【答案】分析：图中有平行线，却无直线同时截AB、CD、EF，所以暂时无法运用平行线的性质转化．
若延长EA交CD于F或延长BA交CE于G，构造三角形或平行线的截线．
解答：
解：延长EA交CD于F．
根据三角形的一个外角等于和它不相邻的两个内角和，得∠EFC=∠C+∠E=79°．
再根据平行线的性质：两条直线平行，同位角相等，得：∠EAB=79°．
故选C．
点评：此题可作的辅助线还可以是：延长BA交CE于G．
运用三角形的外角性质的推论以及平行线的性质即可解决．
若延长EA交CD于F或延长BA交CE于G，构造三角形或平行线的截线．
解答：
解：延长EA交CD于F．根据三角形的一个外角等于和它不相邻的两个内角和，得∠EFC=∠C+∠E=79°．
再根据平行线的性质：两条直线平行，同位角相等，得：∠EAB=79°．
故选C．
点评：此题可作的辅助线还可以是：延长BA交CE于G．
运用三角形的外角性质的推论以及平行线的性质即可解决．
练习册系列答案
相关题目
5、如图所示，AB∥CD，则∠1+∠2+∠3=（ ）
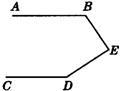24、已知：如图所示，AB∥CD，若∠ABE=130°，∠CDE=152°，则∠BED=
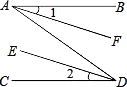如图所示，AB∥CD，需增加什么条件才能使∠1=∠2成立？
如图所示，AB∥CD，EG⊥AB，垂足为G，若∠1=42°，则∠E=