Question

若二次函数y=x²-6x+c的图象经过A（-1，y₁）、B（2，y₂）、C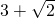（，y₃）三点，则关于y₁、y₂、y₃大小关系正确的是________．

Answer 1

y₁＞y₃＞y₂
分析：根据函数解析式的特点，其对称轴为x=3，图象开口向上；利用y随x的增大而减小，可判断y₂＜y₁，根据二次函数图象的对称性可判断y₃＞y₂；于是y₁＞y₃＞y₂．
解答：A（-1，y₁），B（2，y₂）在对称轴的左侧，y随x的增大而减小，
因为-1＜2，故y₂＜y₁，
根据二次函数图象的对称性可知，C（3+，y₃）中，|3+-3|＞|3-2|，
故有y₃＞y₂；
于是y₁＞y₃＞y₂．
故答案为：y₁＞y₃＞y₂．
点评：本题考查了函数图象上的点的坐标与函数解析式的关系，同时考查了函数的对称性及增减性．