题目内容
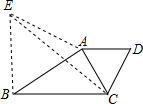
如图，△ADC是等边三角形，B是DC边中点，E在AC延长线上，且CE=BC，请判断△ABE的形状并证明你的结论．
解：∵B是DC边中点，
∴AB是等边三角形ADC的顶角平分线，
∴∠BAC=30°．
∵CB=CE，
∴∠CBE=∠CEB，
∵∠ACD=60°，
∴∠E=30°，
∴∠E=∠BAE，
∴△ABE为等腰三角形．
∴AB是等边三角形ADC的顶角平分线，
∴∠BAC=30°．
∵CB=CE，
∴∠CBE=∠CEB，
∵∠ACD=60°，
∴∠E=30°，
∴∠E=∠BAE，
∴△ABE为等腰三角形．
练习册系列答案
相关题目
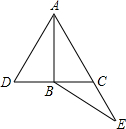如图，△ADC是等边三角形，B是DC边中点，E在AC延长线上，且CE=BC，请判断△ABE的形状并证明你的结论．
如图，△ADC是等边三角形，以点A为中心，把△ABD顺时针旋转60°得到△ACE．连接BE，则△ABE是什么特殊三角形
如图，△ADC是等边三角形，B是DC边中点，E在AC延长线上，且CE=BC，请判断△ABE的形状并证明你的结论．