题目内容
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )


A.2:3 B.2:5 C.3:5 D.3:2
A【考点】相似三角形的判定与性质;三角形的面积;平行四边形的性质.
【专题】探究型.
【分析】先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF,再根据S△DEF:S△ABF=4:10:25即可得出其相似比,由相似三角形的性质即可求出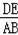
 的值,由AB=CD即可得出结论.
的值,由AB=CD即可得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴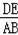
 =
=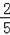
 ,
,
∵AB=CD,
∴DE:EC=2:3.
故选A.
【点评】本题考查的是相似三角形的判定与性质及平行四边形的性质,熟知相似三角形边长的比等于相似比,面积的比等于相似比的平方是解答此题的关键.

练习册系列答案
相关题目



 +
+
 中自变量x的取值范围是( )
中自变量x的取值范围是( )


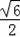
 D.
D.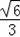
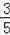

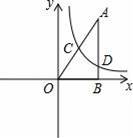

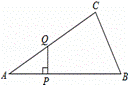
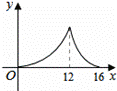
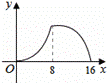
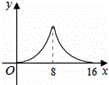
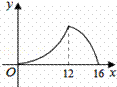
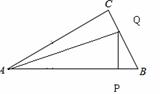 设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )