题目内容
6.分式$\frac{1}{{x}^{2}-3x}$与$\frac{1}{{x}^{2}-9}$通分后的结果是$\frac{x+3}{x(x+3)(x-3)}$,$\frac{x}{x(x+3)(x-3)}$.分析 根据提取公因式可分解x2-3xy,再利用平方差公式分解x2-9,再找系数的最小公倍数,字母的最高次幂,即可得出最简公分母.
解答 解:(1)∵x2-3x=x(x-3),x2-9=(x-3)(x+3),
∴分式$\frac{1}{{x}^{2}-3x}$=$\frac{1}{x(x-3)}$=$\frac{x+3}{x(x+3)(x-3)}$,
分式$\frac{1}{{x}^{2}-9}$=$\frac{1}{(x+3)(x-3)}$=$\frac{x}{x(x+3)(x-3)}$.
故答案为$\frac{x+3}{x(x+3)(x-3)}$,$\frac{x}{x(x+3)(x-3)}$.
点评 本题考查了分式的通分,通分的关键是分解各个分母,找出最简公分母.

练习册系列答案
相关题目
17.已知点(-3,y1),(-2,y2),(2,y3)在函数y=$\frac{-1}{x}$的图象上,则( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
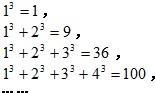
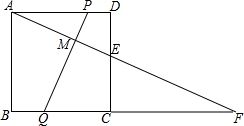 如图,已知正方形ABCD的边长为12,E为边DC上一点,且DE=5.延长AE交BC延长线于点F,点M在线段AE上,且EM=DE,P为边AD上一动点,当点P从点A向点D移动时,PM交边BC于点Q.求PQ:MQ.
如图,已知正方形ABCD的边长为12,E为边DC上一点,且DE=5.延长AE交BC延长线于点F,点M在线段AE上,且EM=DE,P为边AD上一动点,当点P从点A向点D移动时,PM交边BC于点Q.求PQ:MQ.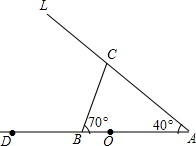 两只猎豹在如图的A处发现有一只野牛离群独自在O处觅食,猎豹打算用迂回的方式,由一只先从A前进到C处,然后再折回到B处截住野牛返回牛群的去路,另一只则直接从A处扑向野牛,已知∠BAC=40°,∠ABC=70°,问,猎豹从C处要转多少度才能直达B处?
两只猎豹在如图的A处发现有一只野牛离群独自在O处觅食,猎豹打算用迂回的方式,由一只先从A前进到C处,然后再折回到B处截住野牛返回牛群的去路,另一只则直接从A处扑向野牛,已知∠BAC=40°,∠ABC=70°,问,猎豹从C处要转多少度才能直达B处? 有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米).另三边用竹篱笆围成,如果竹篱笆的全长为34米.且开有一个1米宽的小门.问鸡场的长和宽各为多少?
有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米).另三边用竹篱笆围成,如果竹篱笆的全长为34米.且开有一个1米宽的小门.问鸡场的长和宽各为多少?