题目内容
如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.
求证:AC=AD.
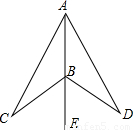
【答案】
证明见解析
【解析】证明:∵∠ABC+∠CBE=180°,∠ABD+∠DBE=180°,∠CBE=∠DBE,∴∠ABC=∠ABD,
在△ABC和△ABD中,∵∠CAE=∠DAE,AB=AB,∠ABC=∠ABD,
∴△ABC≌△ABD(ASA)。∴AC=AD。
根据等角的补角相等可得到∠ABC=∠ABD,再由条件∠CAE=∠DAE,AB=AB可利用ASA证明△ABC≌△ABD,再根据全等三角形对应边相等可得结论。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
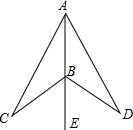 (2012•哈尔滨)如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.
(2012•哈尔滨)如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE. 如图,点B在射线AE上,∠D+∠ABC=180°,若∠CBE=80°,则∠D=
如图,点B在射线AE上,∠D+∠ABC=180°,若∠CBE=80°,则∠D=
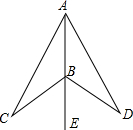 如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.
如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.