题目内容
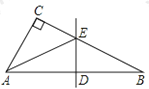
【题目】如图，直线
经过正方形
的顶点
，先分别过此正方形的顶点
、
作
于点
、
于点
．然后再以正方形对角线的交点
为端点，引两条相互垂直的射线分别与
，
交于
，
两点．若
，
，则线段
长度的最小值是___．
【答案】
【解析】
根据正方形的性质可得
，
，然后利用同角的余角相等求出
，再利用“角角边”证明
和
全等，根据全等三角形对应边相等可得
，设
，
，然后列出方程组求出
、
的值，再利用勾股定理列式求出正方形的边长
，根据正方形的对角线平分一组对角可得
，根据同角的余角相等求出
，然后利用“角边角”证明
和
全等，根据全等三角形对应边相等可得
，判断出
是等腰直角三角形，再根据垂线段最短和等腰直角三角形的性质可得
时
最短，然后求解即可．
在正方形
中，，，
，
，
，
，
在和中，
，
，
，
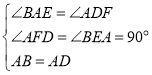设，，
，
，
，
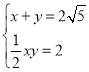消掉并整理得，
，
解得
，
，
当，
，
当，
，
由勾股定理得，
，
在正方形中，，
，
，
，
，
，
，
在和中，
，
，
，
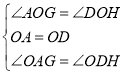是等腰直角三角形，
由垂线段最短可得，时
最短，也最短，
此时，的最小值为
．
故答案为：．
练习册系列答案
相关题目
