Question

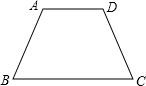
24、学生在讨论命题：“如图，梯形ABCD中，AD∥BC，∠B=∠C，则AB=DC．”的证明方法时，提出了如下三种思路．
思路1：过一个顶点作另一腰的平行线，转化为等腰三角形和平行四边形；
思路2：过同一底边上的顶点作另一条底边的垂线，转化为直角三角形和矩形；
思路3：延长两腰相交于一点，转化为等腰三角形．
请你结合以上思路，用适当的方法证明该命题．

Answer 1

分析：在此以思路一为例进行证明，过点D作DE∥AB交BC于点E，由平行线的性质及已知得到∠DEC=∠C，根据等角对等边得到DE=DC，由已知可得到四边形ADEB是平行四边形，则推出AB=DE，从而可得到AB=DC．

解答：证明：过点D作DE∥AB交BC于点E，
∴∠B=∠DEC，（1分）
又∵∠B=∠C，
∴∠DEC=∠C，
∴DE=DC．（3分）
∵AD∥BC，AB∥DE，
∴四边形ABED为平行四边形，（5分）
∴AB=DE，
∴AB=DC．（6分）

点评：此题是一道开放性的题目，答案不唯一，主要考查学生辅助线的添加及等腰梯形的判定方法的掌握情况．