题目内容
(1)已知如图,点C在线段AB上,线段AC=10,BC=6,点M、N分别是AC、BC的中点,求MN的长度.
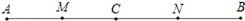
(2)根据(1)的计算过程与结果,设AC+BC=a,其它条件不变,你能猜想出MN的长度吗?请用一句简洁的语言表达你发现的规律;
(3)若把(1)中的“点C在线段AB上”改为“点C在直线AB上”,结论又如何?请说明理由.
(3)若把(1)中的“点C在线段AB上”改为“点C在直线AB上”,结论又如何?请说明理由.
解:(1)∵点M、N分别是AC、BC的中点,
∴CM= AC=5,CN=
AC=5,CN= BC=3,
BC=3,
∴MN=CM+CN=5+3=8;
(2)MN的长度为: a.
a.
∵同(1)可得CM= AC,CN=
AC,CN= BC,
BC,
∴MN=CM+CN= AC+
AC+ BC=
BC= (AC+BC)=
(AC+BC)= a,
a,
即MN的长度就等于AC与BC长度和的一半;
(3)①当点C在线段AB上时,则MN= AC+
AC+ BC=8;
BC=8;
②当点C在线段AB的延长线上时,则MN= AC﹣
AC﹣ BC=5﹣3=2.
BC=5﹣3=2.
∴CM=
 AC=5,CN=
AC=5,CN= BC=3,
BC=3,∴MN=CM+CN=5+3=8;
(2)MN的长度为:
 a.
a.∵同(1)可得CM=
 AC,CN=
AC,CN= BC,
BC,∴MN=CM+CN=
 AC+
AC+ BC=
BC= (AC+BC)=
(AC+BC)= a,
a,即MN的长度就等于AC与BC长度和的一半;
(3)①当点C在线段AB上时,则MN=
 AC+
AC+ BC=8;
BC=8;②当点C在线段AB的延长线上时,则MN=
 AC﹣
AC﹣ BC=5﹣3=2.
BC=5﹣3=2. 
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 中点,函数y=
中点,函数y= 已知如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,请你再添加一个条件
已知如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,请你再添加一个条件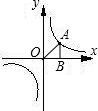 已知如图,点A是反比例函数y=
已知如图,点A是反比例函数y=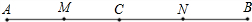
 已知如图,点D在△ABC的边AB上,且DE∥BC,AD=6,BD=12,CE=10.
已知如图,点D在△ABC的边AB上,且DE∥BC,AD=6,BD=12,CE=10.