题目内容
5.已知⊙O的半径是rcm,则其圆内接正六边形的面积是$\frac{3\sqrt{3}}{2}$r2cm2.分析 设O是正六边形的中心,AB是正六边形的一边,OC是边心距,则△OAB是正三角形,△OAB的面积的六倍就是正六边形的面积.
解答 解:如图所示:
设O是正六边形的中心,AB是正六边形的一边,OC是边心距,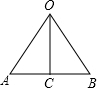
∠AOB=60°,OA=OB=rcm,
则△OAB是正三角形,
∴AB=OA=rcm,
OC=OA•sin∠A=r×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$r(cm),
∴S△OAB=AB•OC=$\frac{1}{2}$×r×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$r2(cm2),
∴正六边形的面积=6×$\frac{\sqrt{3}}{4}$=$\frac{3\sqrt{3}}{2}$r2(cm2).
故答案为:$\frac{3\sqrt{3}}{2}$r2.
点评 本题考查的正多边形和圆、正六边形的性质、等边三角形的判定与性质;理解正六边形被半径分成六个全等的等边三角形是解答此题的关键.

练习册系列答案
相关题目
15. 如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,OE⊥AB于点E,则图中全等的三角形有( )
如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,OE⊥AB于点E,则图中全等的三角形有( )
 如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,OE⊥AB于点E,则图中全等的三角形有( )
如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,OE⊥AB于点E,则图中全等的三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
13.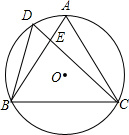 如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AE•BE=CE•ED;③CA2=CE•CD;④CD=BD+AD.其中正确的个数是( )
如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AE•BE=CE•ED;③CA2=CE•CD;④CD=BD+AD.其中正确的个数是( )
 如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AE•BE=CE•ED;③CA2=CE•CD;④CD=BD+AD.其中正确的个数是( )
如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AE•BE=CE•ED;③CA2=CE•CD;④CD=BD+AD.其中正确的个数是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
17. 如图,已知等边△ABC的边上为2,DE是它的中位线,则下面四个结论:①DE=1;②△CDE∽△CAB;③BC边上的高为$\sqrt{3}$;④△CDE的面积与四边形ADEB的面积之比为1:3,其中正确的有( )
如图,已知等边△ABC的边上为2,DE是它的中位线,则下面四个结论:①DE=1;②△CDE∽△CAB;③BC边上的高为$\sqrt{3}$;④△CDE的面积与四边形ADEB的面积之比为1:3,其中正确的有( )
 如图,已知等边△ABC的边上为2,DE是它的中位线,则下面四个结论:①DE=1;②△CDE∽△CAB;③BC边上的高为$\sqrt{3}$;④△CDE的面积与四边形ADEB的面积之比为1:3,其中正确的有( )
如图,已知等边△ABC的边上为2,DE是它的中位线,则下面四个结论:①DE=1;②△CDE∽△CAB;③BC边上的高为$\sqrt{3}$;④△CDE的面积与四边形ADEB的面积之比为1:3,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.由于电力紧张,某地决定对工厂实行鼓励错峰用电.规定:在每天的7:00至24:00为用电高峰期,电价为a元/度;每天0:00至7:00为用电平稳期,电价为b元/度.下表为某厂7、8月份的用电量和电费的情况统计表:
若7月份在平稳期的用电量占当月用电量的$\frac{1}{4}$,8月份在平稳期的用电量占当月用电量的$\frac{1}{5}$,求a、b的值.
| 月份 | 用电量(万度) | 电费(万元) |
| 7 | 8 | 4.4 |
| 8 | 10 | 5.6 |