题目内容

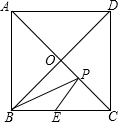如图，在正方形ABCD中，对角线AC，BD相交于O，AB=2，E是BC中点，点P在对角线AC上滑动，则BP+EP的最小值是

A.
$数学公式$
B.
2
C.
$数学公式$
D.
3

C
分析：根据正方形沿对角线的对称性，可得可得无论P在什么位置，都有PD=PB；故均有BP+EP=PD+PE成立；所以原题可以转化为求BP+PD的最小值问题，分析易得连接DE与AC，求得交点就是要求的点的位置；进而可得BP+EP=DE= $\text{[math]}$ = $\text{[math]}$ ，可得答案．
解答：由正方形的对角线互相垂直平分，可得无论P在什么位置，都有PD=PB；
故均有BP+EP=PD+PE成立；
连接DE与AC，所得的交点，即为BP+EP的最小值时的位置，
此时BP+EP=DE= $\text{[math]}$ = $\text{[math]}$ ；故选C
点评：主要考查了正方形中的最小值问题．解决此类问题关键是利用图形的轴对称性把所求的两条线段和转化为一条线段的长度，通常是以动点所在的直线作为对称轴作所求线段中一条线段的对称图形来转化关系．

练习册系列答案

浙江省各地期末试卷精选系列答案

招牌题题库系列答案

怎样学好牛津英语系列答案

运算升级卡系列答案

学业水平标准与考试说明系列答案

云南省小学毕业总复习与检测系列答案

初中学业水平考试复习指导手册系列答案

点击中考系列答案

预学寓练系列答案

标准大考卷系列答案

相关题目

如图：在正方形网格上有△ABC，△DEF，说明这两个三角形相似，并求出它们的相似比．

如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线

，交BC于点E．
（1）求证：点E是边BC的中点；
（2）若EC=3，BD=2

，求⊙O的直径AC的长度；
（3）若以点O，D，E，C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由．

23、如图，在Rt△ABC中，∠BAC=90°，AD=CD，点E是边AC的中点，连接DE，DE的延长线与边BC相交于点F，AG∥BC，交DE于点G，连接AF、CG．
（1）求证：AF=BF；
（2）如果AB=AC，求证：四边形AFCG是正方形．

（2012•陕西）如图，正三角形ABC的边长为3+

．
（1）如图①，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上，在正三角形ABC及其内部，以点A为位似中心，作正方形EFPN的位似正方形E′F′P′N′，且使正方形E′F′P′N′的面积最大（不要求写作法）；
（2）求（1）中作出的正方形E′F′P′N′的边长；
（3）如图②，在正三角形ABC中放入正方形DEMN和正方形EFPH，使得DE、EF在边AB上，点P、N分别在边CB、CA上，求这两个正方形面积和的最大值和最小值，并说明理由．

如图，在Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6

，求另一直角边BC的长．