题目内容
已知线段PA、PB分别切⊙O于A、B两点,AB的度数为120°,⊙O的半径为4,线段AB的长为
- A.8
- B.

- C.

- D.

B
分析:如图,利用切线的性质可以得到PO垂直平分AB,根据弧AB的度数为120°可以得到∠AOP=60°,利用AO=4可以求得AC的长,AB=2AC.
解答: 解:连接PO,交PO于C点,
解:连接PO,交PO于C点,
∵PA、PB分别切⊙O于A、B两点,
∴PO⊥AB,AC=BC,
∵弧AB的度数为120°,
∴∠AOP=∠BOP=60°,
∵⊙O的半径为4,
∴AC=BC=2 ,
,
∴AB=2AC=2×2 =4
=4 ,
,
故选B.
点评:本题考查了切线的性质,解题的关键是正确的利用切线长定理得到PO垂直平分AB.
分析:如图,利用切线的性质可以得到PO垂直平分AB,根据弧AB的度数为120°可以得到∠AOP=60°,利用AO=4可以求得AC的长,AB=2AC.
解答:
 解:连接PO,交PO于C点,
解:连接PO,交PO于C点,∵PA、PB分别切⊙O于A、B两点,
∴PO⊥AB,AC=BC,
∵弧AB的度数为120°,
∴∠AOP=∠BOP=60°,
∵⊙O的半径为4,
∴AC=BC=2
 ,
,∴AB=2AC=2×2
 =4
=4 ,
,故选B.
点评:本题考查了切线的性质,解题的关键是正确的利用切线长定理得到PO垂直平分AB.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
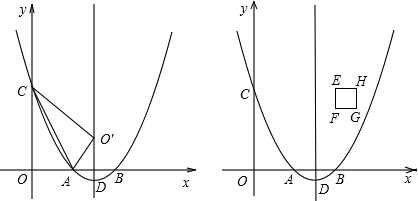
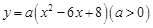 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.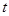 个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出
个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出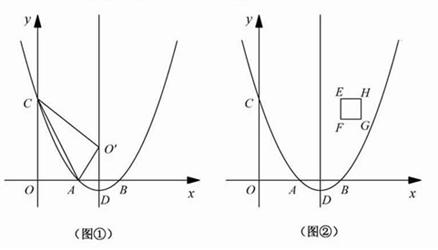
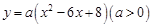 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.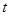 个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出
个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出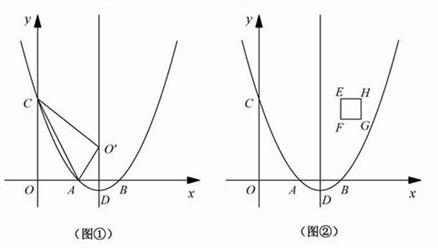
 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.