题目内容
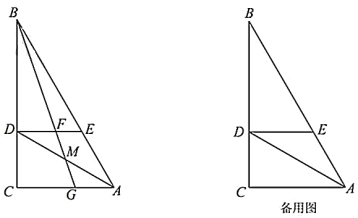
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上的动点,连结
上的动点,连结![]() 并延长分别交
并延长分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
(1)求![]() 的长.
的长.
(2)若点![]() 是线段
是线段![]() 的中点,求
的中点,求![]() 的值.
的值.
(3)请问当![]() 的长满足什么条件时,在线段
的长满足什么条件时,在线段![]() 上恰好只有一点
上恰好只有一点![]() ,使得
,使得![]() ?
?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,满足条件的点
时,满足条件的点![]() 只有一个.
只有一个.
【解析】
(1)由角平分线定义得![]() ,在
,在![]() 中,根据锐角三角函数正切定义即可求得
中,根据锐角三角函数正切定义即可求得![]() 长.
长.
(2)由题意易求得![]() ,
,![]() ,由全等三角形判定
,由全等三角形判定![]() 得
得![]() ,根据全等三角形性质得
,根据全等三角形性质得![]() ,根据相似三角形判定得
,根据相似三角形判定得![]() ,由相似三角形性质得
,由相似三角形性质得![]() ,将
,将![]() 代入即可求得答案.
代入即可求得答案.
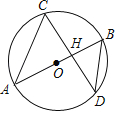
(3)由圆周角定理可得![]() 是顶角为120°的等腰三角形,再分情况讨论:
是顶角为120°的等腰三角形,再分情况讨论:
①当![]() 与
与![]() 相切时,结合题意画出图形,过点
相切时,结合题意画出图形,过点![]() 作
作![]() ,并延长
,并延长![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,![]() ,设
,设![]() 半径为
半径为![]() ,由相似三角形的判定和性质即可求得
,由相似三角形的判定和性质即可求得![]() 长;
长;
②当![]() 经过点
经过点![]() 时,结合题意画出图形,过点
时,结合题意画出图形,过点![]() 作
作![]() ,设
,设![]() 半径为
半径为![]() ,在
,在![]() 中,根据勾股定理求得
中,根据勾股定理求得![]() ,再由相似三角形的判定和性质即可求得
,再由相似三角形的判定和性质即可求得![]() 长;③当
长;③当![]() 经过点
经过点![]() 时,结合题意画出图形,此时点
时,结合题意画出图形,此时点![]() 与点
与点![]() 重合,且恰好在点
重合,且恰好在点![]() 处,由此可得
处,由此可得![]() 长.
长.
(1)解:∵![]() 平分
平分![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]()
(2)解:易得,![]() ,
,![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
由![]() ,得
,得![]() ,
,
∴![]()
∴![]()
(3)解:∵![]() ,过
,过![]() ,
,![]() ,
,![]() 作外接圆,圆心为
作外接圆,圆心为![]() ,
,
∴![]() 是顶角为120°的等腰三角形.
是顶角为120°的等腰三角形.
①当![]() 与
与![]() 相切时,如图1,
相切时,如图1,
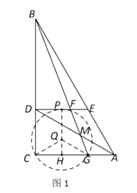
过![]() 点作
点作![]() ,
,
并延长![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,![]()
设![]() 的半径
的半径![]() 则
则![]() ,
,![]() ,
,
解得![]() .
.
∴![]() ,
,![]() .
.
易知![]() ,可得
,可得![]() ,则
,则![]()
∴![]() .
.
②当![]() 经过点
经过点![]() 时,如图2,
时,如图2,
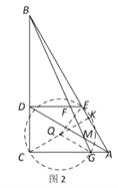
过![]() 点作
点作![]() ,垂足为
,垂足为![]() .
.
设![]() 的半径
的半径![]() ,则
,则![]() .
.
在![]() 中,
中,![]() ,解得
,解得![]() ,
,
∴![]()
易知![]() ,可得
,可得![]()
③当![]() 经过点
经过点![]() 时,如图3,
时,如图3,
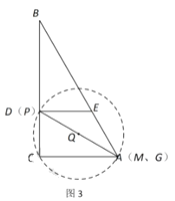
此时点![]() 与点
与点![]() 重合,
重合,
且恰好在点![]() 处,可得
处,可得![]() .
.
综上所述,当![]() 或
或![]() 时,满足条件的点
时,满足条件的点![]() 只有一个.
只有一个.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 30 | … |
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
【题目】重庆市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() ;后4年,每年竣工投入使用的公租房面积
;后4年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 假设每年的公租房全部出租完
假设每年的公租房全部出租完![]() 另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金
另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金![]() 单位:元
单位:元![]() 与时间
与时间![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 满足一次函数关系如下表:
满足一次函数关系如下表:
| 50 | 52 | 54 | 56 | 58 |
|
| 1 | 2 | 3 | 4 | 5 |
|
![]() 求出z与x的函数关系式;
求出z与x的函数关系式;
![]() 求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
![]() 若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高
若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高![]() ,这样可解决住房的人数将比第6年减少
,这样可解决住房的人数将比第6年减少![]() ,求a的值.
,求a的值.
![]() 参考数据:
参考数据: ![]()