题目内容
已知在直角坐标平面内有双曲线y=
,另有△ABC,其中点A、B、C的坐标分别是A(-2
,
),B(-2
,0),C(0,
).
(1)如果将△ABC沿x轴翻折后得到对应的△A1B1C1 (其中点A、B、C的对应点分别是点A1、B1、C1),问:△A1B1C1的三个顶点中,有无在双曲线y=
上的点?若有,写出这个点的坐标.
(2)如果将△ABC沿x轴正方向平移a个单位后,使△ABC的一个顶点落在双曲线y=
上,请直接写出a的值.
(3)如果△ABC关于原点O的对称的三角形△A2B2C2(其中点A、B、C的对应点分别是点A2、B2、C2),请写出经过点A、A2的直线所表示的函数解析式.
6
| ||
| x |
| 2 |
3
| ||
| 2 |
| 2 |
3
| ||
| 2 |
(1)如果将△ABC沿x轴翻折后得到对应的△A1B1C1 (其中点A、B、C的对应点分别是点A1、B1、C1),问:△A1B1C1的三个顶点中,有无在双曲线y=
6
| ||
| x |
(2)如果将△ABC沿x轴正方向平移a个单位后,使△ABC的一个顶点落在双曲线y=
6
| ||
| x |
(3)如果△ABC关于原点O的对称的三角形△A2B2C2(其中点A、B、C的对应点分别是点A2、B2、C2),请写出经过点A、A2的直线所表示的函数解析式.
(1)根据关于x轴对称的点的坐标特点,可得A1的坐标为(-2
,-
),B1的坐标为(-2
,0),A1的坐标为(0,-
),
将三点代入双曲线y=
,只有点A1,符合解析式,此时左边=-
,右边=
=-
,左边=右边.
故有在双曲线上的点,这个点是A1,它的坐标为(-2
,-
);
(2)①平移后点A的对应点在双曲线上,此时点A的对应点的坐标为(-2
+a,
),
代入解析式得:
=
,
解得:a=4
;
②平移后点C的对应点在双曲线上,此时点A的对应点的坐标为(a,
),
代入解析式得:
=
,
解得:a=2
;
综上可得a=2
或a=4
;
(3)点A(-2
,
)关于原点对称的点A2的坐标为(2
,-
),
设过点A、A2的直线解析式为y=kx+b,则
,
解得:
,
故直线AA2的解析式是y=-
x.
| 2 |
3
| ||
| 2 |
| 2 |
3
| ||
| 2 |
将三点代入双曲线y=
6
| ||
| x |
3
| ||
| 2 |
6
| ||
-2
|
3
| ||
| 2 |
故有在双曲线上的点,这个点是A1,它的坐标为(-2
| 2 |
3
| ||
| 2 |
(2)①平移后点A的对应点在双曲线上,此时点A的对应点的坐标为(-2
| 2 |
3
| ||
| 2 |
代入解析式得:
3
| ||
| 2 |
6
| ||
-2
|
解得:a=4
| 2 |
②平移后点C的对应点在双曲线上,此时点A的对应点的坐标为(a,
3
| ||
| 2 |
代入解析式得:
3
| ||
| 2 |
6
| ||
| a |
解得:a=2
| 2 |
综上可得a=2
| 2 |
| 2 |
(3)点A(-2
| 2 |
3
| ||
| 2 |
| 2 |
3
| ||
| 2 |
设过点A、A2的直线解析式为y=kx+b,则
|
解得:
|
故直线AA2的解析式是y=-
3
| ||
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ,另有△ABC,其中点A、B、C的坐标分别是A(
,另有△ABC,其中点A、B、C的坐标分别是A(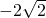 ,
,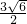 ),B(
),B(