题目内容
 在平面之间坐标系中,一次函数y=-
在平面之间坐标系中,一次函数y=- 的图象与x轴y轴分别相交于A,B两点,在第一象限内是否存在点P,使得以点P,O,B为顶点的三角形与△AOB相似?若存在,请写出所以符合条件的点P的坐标.
的图象与x轴y轴分别相交于A,B两点,在第一象限内是否存在点P,使得以点P,O,B为顶点的三角形与△AOB相似?若存在,请写出所以符合条件的点P的坐标.
解:在y= 中,令x=0,解得:y=2,则B的坐标是(0,2);
中,令x=0,解得:y=2,则B的坐标是(0,2);
在y=- 中令y=0,解得:x=4,则A的坐标是(4,0).
中令y=0,解得:x=4,则A的坐标是(4,0).
当O是直角顶点时,P一定在x轴上,与△AOB重合,不符合题意;
当B是直角顶点时,当△OPB的边OB与△AOB的边BO是对应边时,即△AOB∽△PBO时,P的坐标是(4,2);
当△AOB∽△OBP时, =
= ,即
,即 =
= ,解得:BP=1,则P的坐标是(1,2);
,解得:BP=1,则P的坐标是(1,2);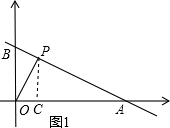
当P是直角顶点,当△AOB∽△OPB时,OP是直角△AOB斜边AB上的高,如图1,
则AB= =
= =2
=2 ,
,
OB2=PB•AB,则BP= =
= =
= ,
,
∴AP=AB-BP=2 -
- =
= ,
,
∴OP= =
= ,
,
过P作PC⊥x轴于点C.
则△PCO∽△AOB,
∴ =
= =
= =
= =
= ,
,
 ∴OC=
∴OC= OB=
OB= ,PC=
,PC= OA=
OA= ,则P的坐标是(
,则P的坐标是( ,
, );
);
当△AOB∽△BPO时,如图2,则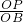 =
= ,即
,即 =
= ,解得:OP=
,解得:OP= ,
,
过P作PD⊥x轴,则△OPD∽△ABO,
∴ =
= =
= =
=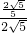 =
= ,
,
则PD= OB=0.4,OD=
OB=0.4,OD= OA=0.8,点P的坐标是(2,1).
OA=0.8,点P的坐标是(2,1).
故P的坐标是:(4,2)或(1,2)或( ,
, )或(0.8,0.4).
)或(0.8,0.4).
分析:首先求得A、B的坐标,然后分O,B,P分别是直角顶点三种情况讨论,每种情况再分那条边与OB是对应边两种情况进行讨论,即可求解.
点评:本题考查了直角三角形相似的判定与性质,正确进行讨论是关键.
 中,令x=0,解得:y=2,则B的坐标是(0,2);
中,令x=0,解得:y=2,则B的坐标是(0,2);在y=-
 中令y=0,解得:x=4,则A的坐标是(4,0).
中令y=0,解得:x=4,则A的坐标是(4,0).当O是直角顶点时,P一定在x轴上,与△AOB重合,不符合题意;
当B是直角顶点时,当△OPB的边OB与△AOB的边BO是对应边时,即△AOB∽△PBO时,P的坐标是(4,2);
当△AOB∽△OBP时,
 =
= ,即
,即 =
= ,解得:BP=1,则P的坐标是(1,2);
,解得:BP=1,则P的坐标是(1,2);
当P是直角顶点,当△AOB∽△OPB时,OP是直角△AOB斜边AB上的高,如图1,
则AB=
 =
= =2
=2 ,
,OB2=PB•AB,则BP=
 =
= =
= ,
,∴AP=AB-BP=2
 -
- =
= ,
,∴OP=
 =
= ,
,过P作PC⊥x轴于点C.
则△PCO∽△AOB,
∴
 =
= =
= =
= =
= ,
, ∴OC=
∴OC= OB=
OB= ,PC=
,PC= OA=
OA= ,则P的坐标是(
,则P的坐标是( ,
, );
);当△AOB∽△BPO时,如图2,则
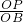 =
= ,即
,即 =
= ,解得:OP=
,解得:OP= ,
,过P作PD⊥x轴,则△OPD∽△ABO,
∴
 =
= =
= =
=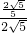 =
= ,
,则PD=
 OB=0.4,OD=
OB=0.4,OD= OA=0.8,点P的坐标是(2,1).
OA=0.8,点P的坐标是(2,1).故P的坐标是:(4,2)或(1,2)或(
 ,
, )或(0.8,0.4).
)或(0.8,0.4).分析:首先求得A、B的坐标,然后分O,B,P分别是直角顶点三种情况讨论,每种情况再分那条边与OB是对应边两种情况进行讨论,即可求解.
点评:本题考查了直角三角形相似的判定与性质,正确进行讨论是关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
 (2013•苏州一模)如图,在平面直角坐标系中,点D为y轴上一点,⊙D与坐标轴分别相交于A(-
(2013•苏州一模)如图,在平面直角坐标系中,点D为y轴上一点,⊙D与坐标轴分别相交于A(- (2012•济宁)如图,在平面直角坐标系中,点P坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
(2012•济宁)如图,在平面直角坐标系中,点P坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( ) 在平面之间坐标系中,一次函数y=-
在平面之间坐标系中,一次函数y=-