题目内容
知数列
的前
项和为
，其中
，
（1）求数列的通项方式.
（2）设数列
的前项和为
，求满足：
的的值.
解：（1）（法一）由
，数列
是以
为首项，2为公比的等比数列，
时，
，当
适合上式，
故
.
（法二）时，
，
时，
，又
，故
（2）由（1）知
，且亦为等比数列，
，由，
或
练习册系列答案
相关题目
，则
=（ ）
9
，
，则下列运算正确的是（ ）
|
| A． | a2+a=2a4 | B． | a3•a2=a6 | C． | 2a6÷a2=2a3 | D． | （a2）4=a8 |
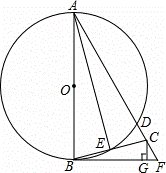
如图，在Rt△ABC中，∠ACB=90°，点D是AB的中点，且CD=
，如果Rt△ABC的面积为1，则它的周长为（ ）
|
| A． |
| B． |
| C． |
| D． |
|
+1下列说法错误的是（ ）
|
| A． | 必然事件的概率为1 |
|
| B． | 数据1、2、2、3的平均数是2 |
|
| C． | 数据5、2、﹣3、0的极差是8 |
|
| D． | 如果某种游戏活动的中奖率为40%，那么参加这种活动10次必有4次中奖 |
受国内外复杂多变的经济环境影响，去年1至7月，原材料价格一路攀升，义乌市某服装厂每件衣服原材料的成本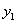
（元）与月份x（1≤x≤7,且x为整数）之间的函数关系如下表：
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 成本（元/件） | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月，随着经济环境的好转，原材料价格的涨势趋缓，每件原材料成本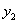
（元）与月份x的函数关系式为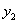=x+62（8≤x≤12,且x为整数）.
(1) 请观察表格中的数据，用学过的函数相关知识求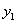与x的函数关系式.
(2) 若去年该衣服每件的出厂价为100元，生产每件衣服的其他成本为8元，该衣服在1至7月的销售量
（万件）与月份x满足关系式=0.1x+1.1（1≤x≤7,且x为整数）; 8至12月的销售量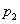
（万件）与月份x满足关系式=
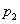－0.1x+3（8≤x≤12，且x为整数），该厂去年哪个月利润最大？并求出最大利润.