题目内容
函数y=-(x+5)2+7的图象的对称轴是直线 .
考点:二次函数的性质
专题:
分析:已知抛物线的顶点式,可知顶点坐标和对称轴.
解答:解:∵y=-(x+5)2+7是抛物线的顶点式,
∴根据顶点式的坐标特点可知,对称轴为直线x=-5,
故答案为:x=-5.
∴根据顶点式的坐标特点可知,对称轴为直线x=-5,
故答案为:x=-5.
点评:本题考查了二次函数的性质,顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h.

练习册系列答案
相关题目
圆内接四边形ABCD的四个内角之比可能是( )
| A、1:2:3:4 |
| B、1:3:4:5 |
| C、2:3:4:5 |
| D、2:3:5:4 |
已知二次函数y=a(x-1)2-b(a≠0)有最小值
,则a、b的大小比较为( )
| 1 |
| 2 |
| A、a>b | B、a<b |
| C、a=b | D、不能确定 |
若一次函数y=kx+3的图象过点P(2,-1),则k的值( )
| A、2 | B、-2 | C、3 | D、-3 |
下列计算正确的是( )
| A、a2+a3=a5 |
| B、a6÷a3=a2 |
| C、(a+b)2=a2+b2 |
| D、(-2a3)2=4a6 |
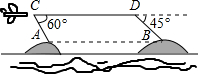 某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得你正前方一海岛顶端A的俯角是60°,然后沿平行与AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是45°,求两海岛间的距离AB.
某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得你正前方一海岛顶端A的俯角是60°,然后沿平行与AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是45°,求两海岛间的距离AB.