题目内容
正方形ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2.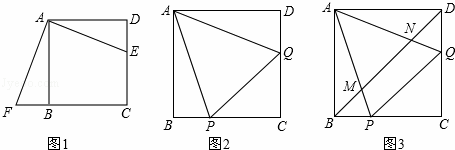
解:(1)∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,
∵DE=BF,∠AFB=∠AED.
故答案为BF,AED;
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°,即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中
∵ ,
,
∴△APE≌△APQ,
∴PE=PQ,
而PE=PB+BE=PB+DQ,
 ∴DQ+BP=PQ;
∴DQ+BP=PQ;
(3)∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK得到MN=MK,
∵∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.



练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
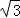 ,
,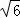 ,﹣3,2
,﹣3,2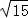 ,3
,3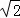 ,…,根据数据排列的规律得到第16个数据应是
,…,根据数据排列的规律得到第16个数据应是 
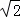 ;将位置①的三角形绕点P1
;将位置①的三角形绕点P1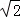 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+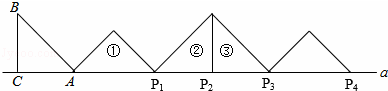

 的相反数是 ,倒数是 ,平方等于 .
的相反数是 ,倒数是 ,平方等于 . +
+ ÷a,其中a=
÷a,其中a= .
.