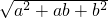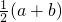题目内容
将sin37°、cos44°、sin41°、cos46°的值按从小到大的顺序排列是________.
sin37°<sin41°<cos46°<cos44°
分析:先把余弦化成正弦,再根据当角是锐角时,正弦值随角度的增大而增大比较即可.
解答:∵cos44°=sin(90°-44°)=sin46°、cos46°=sin(90°-46°)=sin44°,
∴根据当角是锐角时,正弦值随角度的增大而增大得出sin37°<sin41°<cos46°<cos44°,
故答案为:sin37°<sin41°<cos46°<cos44°.
点评:本题考查了锐角三角函数的增减性和互余两角的关系的应用,注意:①如果∠A+∠B=90°,那么sinA=cosB,②当角是锐角时,正弦值随角度的增大而增大.
分析:先把余弦化成正弦,再根据当角是锐角时,正弦值随角度的增大而增大比较即可.
解答:∵cos44°=sin(90°-44°)=sin46°、cos46°=sin(90°-46°)=sin44°,
∴根据当角是锐角时,正弦值随角度的增大而增大得出sin37°<sin41°<cos46°<cos44°,
故答案为:sin37°<sin41°<cos46°<cos44°.
点评:本题考查了锐角三角函数的增减性和互余两角的关系的应用,注意:①如果∠A+∠B=90°,那么sinA=cosB,②当角是锐角时,正弦值随角度的增大而增大.

练习册系列答案
相关题目
 ,
,
 、-
、- 、
、 、
、 、
、


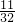
 |等于
|等于