题目内容
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,
连接CD,已知∠CDB=∠OBD=30°.
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.

(1)证明见解析;(2)6 ;(3)6π.
;(3)6π.
【解析】
试题分析:(1)连接OC,OC交BD于E,由∠CDB=∠OBD可知,CD∥AB,又AC∥BD,四边形ABDC为平行四边形,则∠A=∠D=30°,由圆周角定理可知∠COB=2∠D=60°,由内角和定理可求∠OCA=90°,证明切线..
(2)由(1)中的切线的性质和垂径定理以及解直角三角形来求BD的长度.
(3)证明△OEB≌△CED,将阴影部分面积问题转化为求扇形OBC的面积求解.
试题解析:【解析】
(1)证明:如答图,连接OC,OC交BD于E,
∵∠CDB=30°,∴∠COB=2∠CDB=60°.
∵∠CDB=∠OBD,∴CD∥AB.
又∵AC∥BD,∴四边形ABDC为平行四边形.
∴∠A=∠D=30°.
∴∠OCA=180°﹣∠A﹣∠COB=90°,即OC⊥AC.
又∵OC是⊙O的半径,∴AC是⊙O的切线.

(2)由(1)知,OC⊥AC.
∵AC∥BD,∴OC⊥BD. ∴BE=DE.
∵在Rt△BEO中,∠OBD=30°,OB=6,∴BE=OBcos30°=3 .∴BD=2BE=6
.∴BD=2BE=6 .
.
(3)∵在△OEB和△CED中,∠OBE=∠CDE,∠OEB=∠CED,BE=DE,
∴△OEB≌△CED(AAS).∴S阴影=S扇形BOC.
∴S阴影= .
.
答:阴影部分的面积是6π.
考点:1.圆周角定理;2.平行的判定;3. 平行四边形的判定和性质;4.三角形内角和定理;5.切线的判定和性质;6.垂径定理;7. 特殊角的三角函数值;8.负整数指数幂;9.扇形面积的计算;10.转换思想和数形结合思想的应用.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案 的解是正数,则a的取值范围是 .
的解是正数,则a的取值范围是 . ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )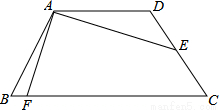
 B.
B. C.
C. D.
D.
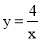 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于
的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于


 B.
B. C.
C. D.
D.