题目内容
13.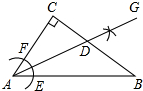 如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧相交于点G;
③作射线AG交BC边于点D.则∠ADB的度数为115°.
④如果AC=5cm,CD=2cm,则D点到AB的距离为2cm.
分析 ③根据角平分线的画法得出AG是∠CAB的平分线,进而结合三角形内角和定理得出∠ADB的度数;
④利用角平分线的性质得出答案.
解答 解:③由题意可得:AG是∠CAB的平分线,
则∠CAD=∠BAD=$\frac{1}{2}$∠CAB=$\frac{1}{2}$×50°=25°,
∵∠C=90°,∠CAB=50°,
∴∠B=40°,
∴∠ADB=180°-25°-40°=115°;
④∵AG是∠CAB的平分线,∠C=90°,CD=2cm,
∴D点到AB的距离为:2cm.
故答案为:115°,2cm.
点评 此题主要考查了基本作图以及角平分线的性质与画法,正确掌握角平分线的性质是解题关键.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | a的倒数是$\frac{1}{a}$ | B. | 任何有理数都有倒数 | ||
| C. | -$\frac{1}{4}$的倒数是-4 | D. | $\frac{1}{2}$的倒数是-2 |
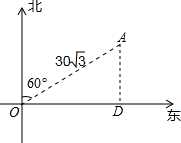 如图,在A岛周围20海里水域内有暗礁,一轮船由西向东航行到O处时,测得A岛在北偏东60°的方向,且与轮船相距30$\sqrt{3}$海里.若该船继续保持由西向东的航向,那么有触礁的危险吗?
如图,在A岛周围20海里水域内有暗礁,一轮船由西向东航行到O处时,测得A岛在北偏东60°的方向,且与轮船相距30$\sqrt{3}$海里.若该船继续保持由西向东的航向,那么有触礁的危险吗?